Modalfrequenzstudie
Alle Dinge schwingen, und wir sind mit vielen Quellen von Schwingungen vertraut, z. B.:
- Musikinstrumente
- Fahrten in einem Auto mit nicht ausgewuchteten Reifen
- Vibrieren eines Flugzeugs, wenn der Pilot die Motoren aufheulen lässt
- Vibrationen unter den Füßen, wenn ein Zug vorbeifährt
Länger anhaltende Schwingungen sind für Strukturen, Fahrzeuge und andere Arten von Maschinen schädlich. Schwingungen sind jedoch häufig unvermeidbar. Unkontrollierte Schwingungen können letztendlich zu Metallermüdung und zum Versagen von Bauteilen oder Strukturen führen. Bei Schwingungen geht es um Frequenzen. Von Natur aus umfassen Schwingungen sich wiederholende Bewegungen. Jedes Auftreten einer vollständigen Bewegungssequenz wird als Zyklus bezeichnet. Die Frequenz wird über die Anzahl der Zyklen in einem bestimmten Zeitraum definiert. Ein Zyklus pro Sekunde entspricht 1 Hertz.
Die Eigenfrequenzen einer Struktur werden durch Zug- oder Druckspannung aufgrund von angewendeten Lasten beeinflusst. Aus diesem Grund umfasst Autodesk Fusion die Option Geladene Modi berechnen. Die Auswirkungen der angewendeten Modi werden ignoriert, wenn diese Option nicht aktiviert ist.
Was sind modale Frequenzen?
Strukturen weisen mehrere Eigenfrequenzen der Schwingung auf, wenn sie durch eine angewendete Kraft, Beschleunigung oder Verschiebung angeregt werden. Die Art und Weise, wie sich die Struktur bei einer bestimmten Eigenfrequenz bewegt, wird als Modusform bezeichnet. Modusformen umfassen Biegen, Verdrehen, Dehnen und Zusammenziehen oder eine Kombination dieser Effekte. Es gibt verschiedene Arten von modalen Frequenzen. Diese lauten wie folgt:
Modi für starren Körper: Oszillierende Bewegung (insbesondere Translation) in den globalen Richtungen oder Drehung um die globalen Achsen. Diese Modi können nur auftreten, wenn das Modell in eine oder mehrere Richtungen nicht mit Abhängigkeiten versehen ist. Das Modell verformt sich nicht, es bewegt sich einfach relativ zu seiner ursprünglichen Position. In manchen Fällen wird durch eine Abhängigkeit das Vibrieren der Struktur in allen möglichen Modusformen verhindert. Deswegen kann es nützlich sein, eine modale Analyse für ein Modell ohne Abhängigkeiten auszuführen, auch wenn die Starrkörpermodi normalerweise nicht von Bedeutung sind.
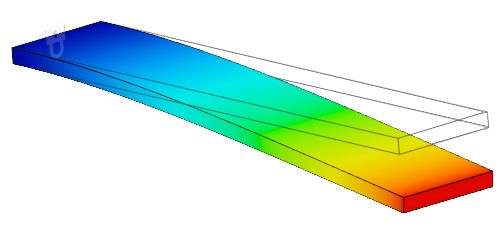
Grundlegende Modi: Der erste Modus (tiefste Frequenz) - (ausgenommen Starrkörpermodi). Die Form eines Sprungbretts, wenn jemand am äußeren Ende steht, ähnelt beispielsweise dem ersten grundlegenden Schwingungsmodus:
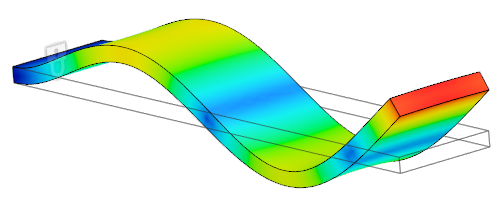
Harmonische Modi: In der Regel ein Vielfaches der grundlegenden Modi. Harmonische Modusformen sind komplexer als grundlegenden Modi und weisen mehr Wendepunkte auf. Um auf das Beispiel des Sprungbretts zurückzukommen, wird hier ein Bild der zweiten Harmonischen des grundlegenden Schwingungsmodus gezeigt. Es gibt zwei Wendepunkte entlang der Länge (dunkelblau), wobei das verankerte Ende des Bretts nicht mitgerechnet wird:
Für einen Modus kann es eine einfache Auf-und-ab-Bewegung geben. Bei einer höheren Frequenz kann dann eine einfache Bewegung von einer Seite zur anderen oder von vorne nach hinten auftreten. Zwischen diesen einfachen grundlegenden Modi können wir möglicherweise eine oder mehrere harmonische Schwingungsmodi entdecken. Daher wird die Form bei jedem nachfolgenden Modus (jeder höheren Frequenz) nicht unbedingt immer komplexer. Im Allgemeinen zeigt sich jedoch der Trend, dass Formen mit steigender Schwingungsfrequenz immer komplexer werden.
Die folgenden Faktoren beeinflussen die Eigenfrequenzen und Modusformen:
- Die Form der Struktur
- Die Masse der Struktur und die Masseverteilung
- Die Art und Weise, wie die Struktur beschränkt ist
- Die Steifheit des Materials und der Struktur
- Die Zug- oder Drucklasten, die auf die Struktur angewendet werden
Denken Sie an die Saite eines Klaviers, einer Gitarre oder einer Geige. Je größer die Masse der Saite ist, desto tiefer ist die Schwingungsfrequenz. Hingegen gilt, je größer die Spannung der Saite, desto höher die Schwingungsfrequenz. Die stärkste Schwingung ist der erste grundlegende Modus (oder die Grundfrequenz). Dabei bewegt sich die ganze Saite in einer einfachen Bogenform vor und zurück. Für den ersten harmonischen Modus wird die Form der Saite zu einer S-Kurve. Das heißt, dass es auf halber Länge einen Wendepunkt gibt und die Hälften der Saite sich in entgegengesetzte Richtungen bewegen. Obertöne treten auf, wenn eine Schwingung mit höherer Frequenz einen niedrigeren Frequenzmodus überlagert.
Warum werden Modalfrequenzanalysen durchgeführt?
Es kann mit ernsten Konsequenzen verbunden sein, wenn eine Stromquelle wie z. B. ein Motor eine Frequenz erzeugt, mit der die daran befestigte Struktur von Natur aus vibriert. Wenn ein Objekt durch eine Eigenfrequenz angeregt wird, wird die Schwingung noch verstärkt. Dieses Phänomen wird als Resonanz bezeichnet. Wenn Schwingungen Resonanz in einem Objekt verursachen, kommt es zur Zerstörung, es sei denn, die Bauteile sind dafür konstruiert, die Spannung auszuhalten.
Ingenieure müssen bei der Konstruktion beachten, dass beim normalen Betrieb von Maschinen keine Resonanz auftritt. Dies ist der Hauptzweck der Modalfrequenzanalyse. Im Idealfall sollte der erste Modus eine Frequenz höher als mögliche Antriebsfrequenzen liegen. Alternativ können die Antriebsfrequenzen bei den verschiedenen Betriebsdrehzahlen die Eigenfrequenz überschreiten. In so einem Fall muss die Konstruktion die momentane Resonanz aushalten, die auftritt, während die Maschine auf die Betriebsdrehzahl beschleunigt wird.
In einigen speziellen Fällen soll eine Konstruktion mit Resonanz reagieren. Ein Beispiel dafür ist ein Ultraschallreinigungsgerät. Um die erforderliche Energie zu minimieren, die für die Vibration des Geräts benötigt wird, und die Größe der Schwingung zu maximieren, wird die Struktur durch eine Eigenfrequenz angeregt.
Unabhängig davon, ob das Ziel in der Vermeidung oder der Erzeugung von Eigenfrequenzen besteht, ist eine Modalfrequenzsimulation ein wichtiger Bestandteil des Konstruktionsprozesses.