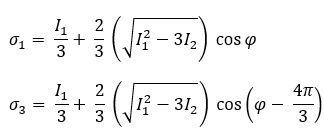Hauptspannungsberechnungen
Spannungen können basierend auf Achsen berechnet werden, die sich von den globalen X-, Y- und Z-Richtungen unterscheiden. Das Koordinatensystem kann gedreht werden, sodass nur lotrechte Spannungen verbleiben und alle Scherspannungen gleich null sind. Bei dieser Ausrichtung sind der Normalvektor einer Fläche und der Spannungsvektor auf dieser Fläche kollinear. Die Richtung des Normalvektors wird dann als Hauptspannungsrichtung bezeichnet. Die Größe des Spannungsvektors auf der Fläche wird als Hauptspannungswert bezeichnet. Es gibt drei Hauptspannungswerte: die 1., 2. und 3. Hauptspannung. Diese Werte werden oft als maximale, mittlere bzw. minimale Hauptspannung bezeichnet.
Die mathematischen Gleichungen für die Bestimmung der Hauptspannungen (σ1 und σ3) sind komplizierter als die zuvor angegebene Von-Mises-Spannungsgleichung. Zunächst muss der Drehwinkel (φ) in Bogenmaß zwischen der globalen und der Hauptachse bestimmt werden:
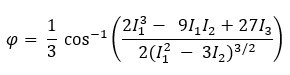
wobei I1, I2 und I3 Spannungsinvarianten darstellen, die durch die folgenden Gleichungen bestimmt werden:
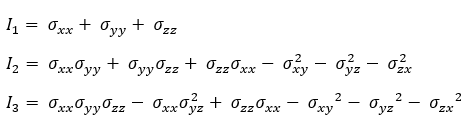
Die erste und die dritte Hauptspannung werden mithilfe der folgenden Gleichungen bestimmt: