Theorie zu quasi-statischen Ereignissimulationsstudien

Dieser theoretische Hintergrund gilt sowohl für dynamische als auch für quasi-statische Ereignissimulationen.

Ereignissimulationen kombinieren die Prinzipien des hookeschen Gesetzes (F = -kx) und des zweiten newtonschen Gesetzes (F = ma). Wenn wir diese beiden Gleichungen kombinieren, indem die Kraft eliminiert wird, erhalten wir ma + kx = 0. Jetzt können wir die Auswirkungen der Dämpfung (F = -cv) hinzufügen, um die allgemeine Gleichung der Bewegung zu erhalten:

ma + cv + kx = 0

Dabei gilt: m ist die Masse, a ist die Beschleunigung, c ist ein Dämpfungskoeffizient, v ist die Geschwindigkeit, k ist die Steifheit und x ist die Verschiebung. In Matrix-Form wird diese Gleichung wie folgt dargestellt:

[M]{a} + [C]{v}+[K]{x} = 0

Aus dieser grundlegenden Gleichung können durch Verwendung des Verschiebungsvektors {x} und den Konstitutivgesetzen für die Materialreaktion Spannungen und Dehnungen bestimmt werden.

Zeitintegration für zentralen Unterschied

Bei Ereignissimulationen wird ein expliziter Solver verwendet, der auf dem Algorithmus zur Zeitintegration für den zentralen Unterschied basiert. Dieser Algorithmus verwendet Kenntnisse der beiden vorherigen Status, um den aktuellen Status direkt zu lösen (Verschiebung, Geschwindigkeit und Beschleunigung). Die Größe des Schritts von einem Zustand zum nächsten wird durch die Courant-Zahl der Stabilität (stabiles Schrittintervall) gesteuert, die den größten zulässigen Schritt bestimmt, bei dessen Überschreitung die Lösung fehlschlägt. Wenn die Auswirkungen der Dämpfung berücksichtigt werden, wird dies wie folgt ausgedrückt:

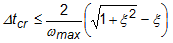
Dabei ist Δtcr die stabile Schrittweite, ωmax die größte Eigenfrequenz im Netz und ξ der Bruchteil der kritischen Dämpfung im höchsten Modus.

Im Allgemeinen sind stabile Schrittweiten in einer quasi-statischen Ereignissimulation sehr klein. Der explizite Solver ist sehr effizient und kann relativ gut mit Material- und Kontakt-Nichtlinearitäten umgehen, da bei den einzelnen Iterationen keine Steifheitsmatrix gebildet werden muss. Knotenbeschleunigungen können direkt gelöst werden.