Verbinder zwischen starren Körpern

Ein Verbinder zwischen starren Körpern verbindet die Translationsfreiheitsgrade mehrerer Körper miteinander. Die Abhängigkeit Verbinder zwischen starren Körpern steht für die folgenden Simulationsanalysen zur Verfügung:

Symbol Bearbeiten Statische Spannung

Symbol Bearbeiten Modale Frequenzen

Symbol Bearbeiten Strukturelle Knickung

Symbol Bearbeiten Nichtlineare statische Spannung

Symbol Bearbeiten Quasi-statische Ereignissimulation

Symbol Bearbeiten Dynamische Ereignissimulation

Anmerkung: Bei einer Verbindung mit Volumenkörpern wird die Drehung an den Ansatzpunkten nicht durch starre Verbinder beschränkt. Wenn ein starrer Verbinder beispielsweise an einer geraden Kante eines Volumenkörpers angesetzt ist, kann sich der Körper frei um diese Kante drehen. Eine gerade Linie mit Netzpunkten ohne Torsionssteifigkeit stellt einen Angelpunkt dar.

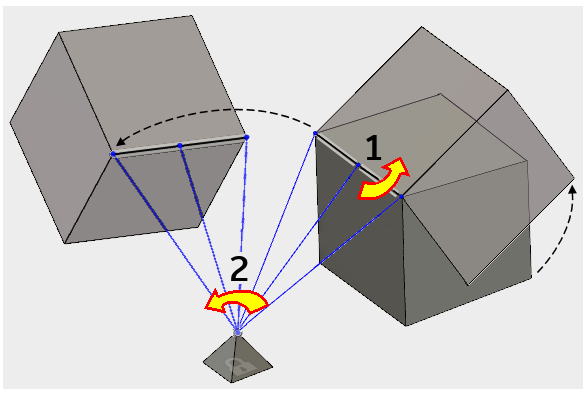
Sehen Sie sich das Beispiel in der folgenden Abbildung an: Der Würfel kann sich um die Kante drehen, an die der starre Verbinder angesetzt ist (als 1 in der Abbildung dargestellt). Der starre Verbinder und der Würfel können sich außerdem frei um den Ankerpunkt an der Spitze der Pyramide drehen (als 2 in der Abbildung dargestellt). Die Scheitelpunkte und Kanten beider Volumenkörper können eine Drehbewegung nicht verhindern. Die Spitze der Pyramide verhält sich wie ein Kugelgelenk, sodass eine Drehung des Verbinders und des angesetzten Körpers in eine beliebige Richtung möglich ist.

Diagramm Starre Verbindung zwischen Volumenkörpern

Um diese Bewegung nur mit starren Verbindern zu verhindern, sind drei Verbinder zwischen starren Körpern erforderlich:

Ein Verbinder zwischen einem Ankerpunkt auf der Pyramide und mindestens drei nicht kollinearen Punkten, zwei Kanten oder einer Fläche auf dem Würfel
Ein Verbinder zwischen einem weiteren Scheitelpunkt auf der Pyramide und einem Punkt, einer Kante oder Fläche auf dem Würfel
Ein Verbinder zwischen einem dritten Scheitelpunkt auf der Pyramide und einem Punkt, einer Kante oder Fläche auf dem Würfel Die drei Ankerpunkte dürfen nicht kollinear sein, ansonsten würden Sie einen Angelpunkt bilden.

Alternativ können Sie den zweiten oder dritten Ankerpunkt der starren Verbinder an Scheitelpunkten auf separaten Volumenkörpern ansetzen, solange die drei Ankerpunkte nicht kollinear sind.