Quasi-static curves with different rates of displacement
The two curves shown in Figure 1 have a different number of steps AND define different rates of displacement. Despite the apparent shape of the curves, Figure 1(a) prescribes a faster rate of displacement in the first step.
The curve in Figure 1(a) defines a transition in
- step 1 from 0 to a 0.5 multiplier of the full displacement.
Meanwhile the curve defined in Figure 1(b) defines a transition
- step 1 from 0 to a 0.25 multiplier of the full displacement.
The result is that after step 1, the left body has deflected further than the right body.
 |
 |
| Figure 1(a) 2-step multiplier curve. In actuality, the 2nd step is elongated to match 1(b) | Figure 1(b) 4-step multiplier curve. This curve controls the shape of the curve in 1(a) |
The curve in Figure 1(a) then defines a linear deflection from the 0.5 multiplier to the full deflection over the rest of the duration.
The curve in Figure 1(b) also defines a linear transition to the full deflection over the rest of the duration, but it is starting from 0.25 multiplier of the full deflection.
Since both curves end at the same point, the result is that deflection on the left body is greater in the first step, but the velocity of the subsequent deflection is greater in the right body so that they can end with the same deflection at the same time.
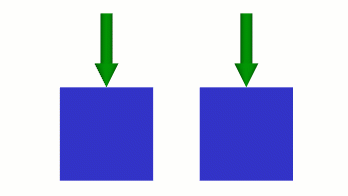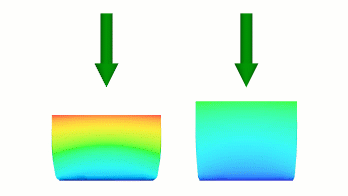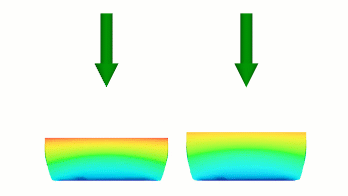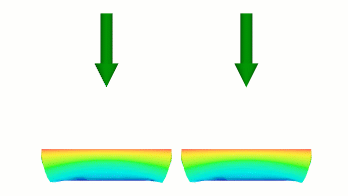 |
Figure 2 Curves with different steps, defining different rates of displacement.