Constraining a thermal analysis

When running simulations it is important to constrain the analysis properly. When the analysis is overconstrained the solver has too few variables to solve the it properly. When the analysis is underconstrained the solver doesn't have enough information to calculate all the variables.

Properly constrained analyses

Properly constrained analyses allow the energy to balance, energy into the analysis must equal energy out of the analysis. An analysis must contain a temperature, convection, or radiation load to provide a reference temperature. Any thermal load can suffice as the heat source or heat sink when coupled with a temperature referencing load.

Overconstrained analysis

Overconstraining an analysis happens when you have either entered too much information across the model or at a single location. As mentioned in the Thermal Loads page the same surface can't contain a temperature and another thermal load. The software prevents you from applying a temperature and another thermal load to the same surface. Two adjacent surfaces are permitted. Having two different load conditions at any location on a model is still over constraining the model.

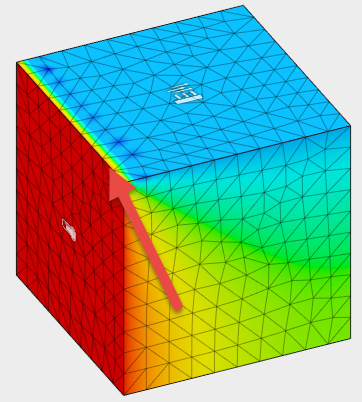
overconstrained example

Note: In the previous image, a temperature constraint is placed on an adjacent face to a film coefficient. The vertex under the arrow is overconstrained. Notice that the nodes one element in from the vertex that the two faces meet have a lower temperature. These low temperature nodes are the effect of the overconstrained vertex.

Note: Avoid having thermal conditions that share any portion of the geometry. The model can corrected by adding a small chamfer to separate the faces with loads applied or splitting one of the surfaces.

Underconstrained analysis

Underconstraining an analysis is the opposite of overconstraining an analysis and there are not enough loads to properly solve the analysis. There can be several outcomes depending on which thermal loads are applied.

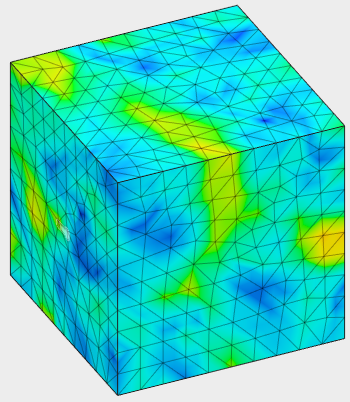
If there is only one temperature referenced in the model and no other heat load, then the model has no heat flow or temperature gradient. This type of load case can cause a thermal gradient to look like the following:
A model without a load that references a temperature in the analysis, it fails to solve. Warnings should appear in the solve dialog.

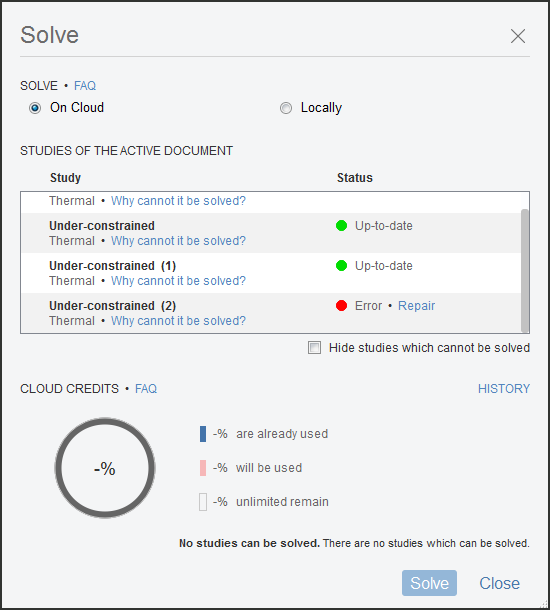
More information can be found by clicking the Repair link.

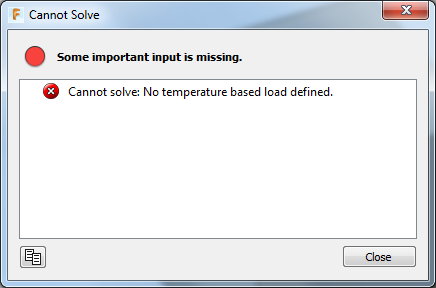
Analyses setup without a temperature-based load defined can not have a temperature gradient because there is no reference.