The Laurenson procedure can be applied to rural and urban catchments in both design storm and continuous simulation situations. It allows for the non-linear response from catchments over a large range of event magnitudes.
The Laurenson procedure is also known as the RAFTS method, and is originally from a paper Aitken, A.P. (1975). However the equation is repeated in ARR Volume 1 on page 187. See also the reference Sobinoff et.al. (1983). The equation is only suitable for an n value of 0.025.
Further modifications were made by Willing and Partners following calibration runs on project catchments between 1976 and 1985.
The hydrological data requirements are: catchment area, slope, degree of urbanization, loss rates, observed, or design rainfall.
These data are used to compute the storage delay coefficient for each of the subcatchments and hence to develop the non-linear runoff hydrograph. A default exponent is adopted, although you may override this value with either a different non-linear exponent or a rating table of flow vs an exponent to define different degrees of catchment non-linear response.
More information about the various equations used are provided in the sections below.
Initial Rainfall Loss - Specifies the depth of rainfall that infiltrates before any runoff occurs.
Continuous Rainfall Loss - Specifies the loss that occurs after the initial loss has been satisfied.
B - This can be entered or calculated from the equation in section "Coefficients B and n" below.
n - Storage non-linearity exponent by default is set to -0.285
Adapt Factor - Can be used as a multiplication factor used during calibration to modify the calculated B. It will default to value of 1.
Manning's n - PERN is an adaption factor used to introduce the effect of pervious catchment roughness as follows:
|
n |
PERN |
|---|---|
|
0.010 |
0.4 |
|
0.015 |
0.5 |
|
0.025 |
1.0 |
|
0.100 |
3.0 |
Degree Urbanization - Fraction of catchment urbanized.
Catchment Slope - Modified equal area slope (%).
Percent Impervious - Impervious portion of the Inflow area.
Urban Creep - This scales the impermeable area by the amount specified. This can be used to take the increase of urban areas, or other factors into account. This value is only enabled (and used) when the analysis creep of the Analysis Criteria is set to "Use Catchment Areas ".
Storage-Discharge Relationship
Each subarea is treated as a concentrated conceptual storage. Each storage has a storage delay time described thus:
K(q) = Bqn
where :
K(q) = subarea storage delay time (hours) as a function of q
q = discharge (m3/s)
B = storage delay time coefficient
n = storage non-linearity exponent
Substituting the cascading non-linear storage equation into the storage delay time equation gives:
s = Bqn + 1
where:
s = volume of storage (hrs x m3/s)
B = storage delay time coefficient
n = storage non-linearity exponent. By default is set to -0.285
The rainfall is applied to each subarea, an excess computed and the excess converted into an instantaneous inflow. This instantaneous flow is then routed through the subarea storage to develop an individual subcatchment outlet hydrograph.
The default value for the non-linearity exponent is -0.285. The application provides the mechanisms to alter this value, usually in respect to rare events involving significant subcatchment overbank flood routing, by:
- Directly entering an amended value of "n". A value of zero would indicate linear catchment response and equate with unit hydrograph theory.
- Entering an "n" = f (Q) rating curve for each subcatchment.
In this manner, the application can simulate either a linear or non-linear response.
Coefficients B and n
B is either directly input for each subcatchment or estimated from the equation below, which was derived by Aitken (1975). The value of B for each subarea is assumed to equal the average value of B for the subcatchment.
BAV = 0.285 A0.52 (1 + U)-1.97 Sc-0.50
where :
B = mean value of coefficient B for subcatchment
A = subcatchment area (km²)
U = fraction of catchment that is urbanised. (Where U = 1.0, the catchment is fully urbanised and when U = 0.0, the catchment is completely rural)
Sc = main drainage slope of subcatchment (%). (The longest path of the subcatchment, starting at subcatchment outlet running up the main channel then if necessary branching off at the furthest tributary, to the top of the subcatchment.)
This equation was initially derived from six urban catchments in Australia with the following ranges applying:
A varied from 0.8 km² to 56 km²
U varied from 0.0 to 1.00
Sc varied from 0.22% to 2.90%.
However, over the succeeding years a wide range of areas, slopes and urbanization outside these ranges have been tested with a high degree of success. See Sobinoff et al (1983).
For gauged catchments, deduced B values, evaluated as the average value from recorded rainfall/runoff events, should be used in preference to generalized regression estimates.
As U in certain instances can be rather vague, data input in this respect has been amended to include a % impervious (%I) parameter for each subcatchment in place of the U term.
The model interprets U in terms of %I based on the following ratios:
| %I | U |
|---|---|
| 0 | 0 |
| 30 | 0.7 |
| 50 | 1.0 |
| 100 | 2.0* |
*This value is extrapolated from the original data based on limited results from fully impervious areas.
B Modification Factors
Where gauged rainfall/runoff data is available for a range of events, it should be used in preference to the above regression equation with modifying factors.
PERN
The original regression equation (as expressed in section "Coefficients B and n") does not differentiate between catchments with the same degree of urbanization but different roughness. An additional empirical parameter has therefore been added to take pervious subcatchment roughness into account.
The parameter PERN is inputted as a Mannings 'n' representation of the average subcatchment roughness. B is then modified in accordance with the following table. If PERN is left blank, then B is unchanged.
|
n |
PERN |
|---|---|
| 0.010 | 0.4 |
| 0.015 | 0.5 |
| 0.025 | 1.0 |
| 0.100 | 3.0 |
It is common for a split subcatchment analysis to estimate a lower subcatchment peak than a peak using only a lumped (impervious plus pervious component) subcatchment definition.
Based on a study calibrating urban catchments in Canberra, the surface runoff routing parameters for PERN Manning's roughness for impervious and pervious areas are 0.015 and 0.040 respectively. (Willing and Partners, 1993)
BX
During calibration of a gauged catchment, an additional parameter BX in the header data is included to modify the calculated or input B by a further multiplication factor. The parameter BX will then uniformly modify all subcatchment B values previously computed, or set in the equation expressed in section "Coefficients B and n".
Routing Method
Routing for a particular subcatchment is carried out using the Muskingum-Cunge method. The storage is considered to be a non-linear function of the discharge.
s = K(q) x q Equation (1)
where:
s = volume of storage (hr × m³/s)
q = instantaneous rate of runoff (m³/s)
K(q) = storage delay time as a function of q (hours)
The storage function is used in the continuity equation in finite difference form:
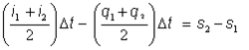Equation (2)
where:
i1, i2 = Inflow at beginning and end of routing period (m³/s)
delta t = routing interval (hr)
q1, q2 = outflow from the storage at beginning and end of routing period (m³/s)
s1, s2 = storage volume at beginning and end of routing period (hr × m³/s)
Substituting s2 and s1 in Equation (2) from Equation (1) gives:
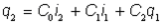
where:
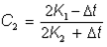
An iterative solution is required due to the interrelation between C0, C1, C2, K2 and q2. K1 and K2 are the computed subarea storage delay times as a function of q at the beginning and end of the iteration respectively.
Routing Details
Puls' level pool routing procedure is used in the retarding basin module. The inflow hydrograph is routed through the basin using the storage routing described below:
where:
i1, i2 = inflows at times 1 & 2 (m³/s)
s1, s2 = total storage at times 1 & 2 (m³)
O1, O2 = outflows at times 1 & 2 (m³/s)
delta t = routing interval(s)
Subscripts 1 and 2 refer to the beginning and end of the routing interval respectively.
References
Aitken, A.P. (1975) Hydrologic investigation and design of urban stormwater drainage systems. Aust. Water Resources Council Tech. Paper No. 10, Dept of the Environment and Conservation, A.G.P.S., Canberra.
Institution of Engineers, Australia. (1987) Australian Rainfall and Runoff - A Guide to Flood Estimation (edited by D.H. Pilgrim and R.P. Canterford), Volumes 1 and 2, Revised Edition, November, 1987, Canberra
James 1998, Editor Modeling the Management of Stormwater Impacts Volume 6 Chapter 23 Author Ashok Pandit and Joanie Regan What is the Impervious Area Curve Number. Publisher CHI Guelph Ontario Canada.
Laurenson E.M. (1964) A Catchment Storage Model for Runoff Routing, Journal of Hydrology, Volume 2, pp 141-163
Sobinoff, P. Pola, J.P. and O’Loughlin, G.C. (1983) Runoff routing parameters for the Newcastle-Sydney-Wollongong region. Hydrol. And Water Resources Symposium 1983, inst. Engrs Aust., Natl Conf. publ. No. 83/13, pp. 28-32. T
USDA National Resources Conservation Service, 1986, Urban Hydrology for Small Watersheds, Technical Release 55.
Viessman W. et al 1977, Introduction to Hydrology", Harper&Row Publishers New York
WEF 1992, Manual of Practice FD-20 Design and Construction of Urban Stromwater Management Systems ASCE and WEF ISBN 0-87262-855-8