Fundamentos teóricos de las frecuencias modales

El proceso matemático que se sigue para determinar las frecuencias naturales y las formas de modo correspondientes analizando elementos finitos es complejo. Para que la teoría sea más fácil de entender, consideraremos el sistema de una masa del muelle lineal muy simple con un grado de libertad (GDL). Es decir, la masa solo se puede mover libremente en una única dirección.

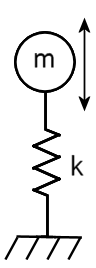
En la imagen siguiente, m es la masa y k es la rigidez del muelle:

diagrama del sistema con la masa del muelle con grado de libertad

La ley de Hooke define la fuerza (F) necesaria para desplazar un muelle con una rigidez (k) a una distancia (X):

(1) F = k·X

La segunda ley de movimiento de Newton especifica la relación entre la fuerza (F), la masa (m) y la aceleración (a) para nuestro sistema único de grados de libertad:

(2) F = m·a

Al combinar estas dos ecuaciones, tenemos una relación entre masa (m), aceleración (a), rigidez del muelle (k) y desplazamiento (X):

(3) m·a = k·X

La siguiente ecuación nos proporciona la frecuencia angular de oscilación (), en radianes por segundo; para este sistema de masa del muelle lineal simple:

(4) ω = (k/m)1/2

Hay 2π radianes por ciclo de vibración. Por lo tanto, la siguiente ecuación nos proporciona la frecuencia natural de oscilación (fn), en hercios:

(5) fn = (k/m)1/2 / (2·π)

En un modelo real de elementos finitos, tenemos movimiento 3D y muchos grados de libertad debido a todos los nodos y elementos de la malla.

Nota: No se tiene en cuenta la amortiguación en el cálculo de la frecuencia natural. La amortiguación se define como una disminución de la amplitud de la oscilación debido a la energía que se drena del sistema. La energía se pierde cuando se superan fuerzas de fricción, viscosas u otras fuerzas de resistencia. La amortiguación que se produce en materiales de fabricación típicos (como acero, aluminio y hormigón) es baja. Por lo tanto, la frecuencia natural sin amortiguación no suele estar lejos de la frecuencia natural real. La amortiguación reduce la frecuencia de vibración a diferencia de un sistema sin amortiguación.

En un sistema continuo, el número de modos de vibración es infinito. Sin embargo, en un modelo de elementos finitos, hay un número finito de grados de libertad y, por tanto, un número finito de modos de vibración. Determinar las frecuencias de vibración y las formas de modo para estos complejos sistemas 3D implica operaciones de matriz, valores propios y vectores propios.

La ecuación (4) es un problema de valores y vectores propios con un número finito de soluciones. La frecuencia angular (ω) es una cantidad escalar. En las soluciones en particular, todos los grados de libertad oscilan a la misma frecuencia angular. Sin embargo, la amplitud de la vibración (δ) es una cantidad vectorial. En este sistema complejo, δ es análogo al desplazamiento (X) en nuestro ejemplo con el grado de libertad único. Los distintos grados de libertad oscilan con diferentes amplitudes, dadas por los componentes de δ . Esta variación de amplitud nos proporciona la forma del modo.

La definición adecuada de los valores propios, los vectores propios y las operaciones matemáticas utilizadas para resolver un análisis modal están fuera del ámbito de este tema.