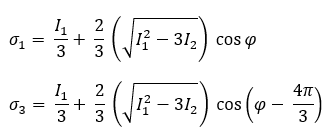Cálculos de la tensión principal

Las tensiones se pueden calcular en función de un conjunto de ejes que difieren de las direcciones globales X, Y y Z. Podemos rotar el sistema de coordenadas para que solo se mantengan las tensiones normales y todos los esfuerzos de cizalla sean cero. Con esta orientación, el vector normal de una superficie y el vector de tensión que actúa sobre esa superficie son colineales. A continuación, la dirección del vector normal se denomina dirección de la tensión principal. La magnitud del vector de tensión en la superficie recibe el nombre de valor de tensión principal. Existen tres valores principales de tensión: Primera, segunda y Tercera tensión principal. Estos valores se suelen denominar Tensión principal máxima, Intermedia y Mínima, respectivamente.

Las ecuaciones matemáticas para determinar las tensiones principales (1 y 3) son más tediosas que la ecuación de tensión de Von Mises especificada anteriormente. Primero debemos determinar el ángulo de rotación (φ), en radianes, entre los ejes global y principal:

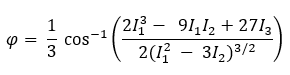
donde I1, I2 y I3 son invariantes de tensión determinados por las siguientes ecuaciones:

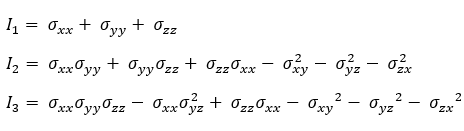
Por último, las tensiones principales primera y tercera se determinan mediante las siguientes ecuaciones: