Teoría de simulación cuasiestática de eventos

Este contexto teórico es válido tanto para simulaciones dinámicas como cuasiestáticas de eventos.

Las simulaciones de eventos combinan los principios de la ley de Hooke (F=-kx) y la segunda ley de Newton (F=ma). Después de combinar estas dos ecuaciones eliminando el término de fuerza, llegamos a ma + kx = 0. Ahora podemos añadir los efectos de la amortiguación (F=-cv) para llegar a la ecuación general de movimiento:

ma+cv+kx = 0

donde m es la masa, a es la aceleración, c es un coeficiente de amortiguamiento, v es la velocidad, k es la rigidez y x es el desplazamiento. En formato de matriz, esta ecuación se representa como:

[M]{a} + [C]{v}+[K]{x} = 0

A partir de esta ecuación fundamental, las tensiones y las deformaciones se pueden determinar con el vector de desplazamiento {x} y las leyes constitutivas que rigen la respuesta del material.

Integración de tiempo central con diferencias

Las simulaciones de eventos utilizan un solucionador explícito basado en el algoritmo de integración de tiempo central con diferencias. Este algoritmo utiliza lo que sabe de los dos estados anteriores para resolver directamente el estado actual (desplazamiento, velocidad y aceleración). El tamaño del paso de un estado al siguiente está determinado por el límite de estabilidad de Courant (incremento de paso estable), que controla el paso más grande permitido, más allá del cual la solución fallará. Cuando se tienen en cuenta los efectos de la amortiguación, se expresa de la siguiente manera:

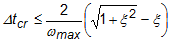
Donde Δtcr es el incremento de paso estable, ωmax es la frecuencia natural más grande de la malla y ξ es la fracción de la amortiguación crítica en el modo más alto.

En general, los incrementos de pasos estables en una simulación cuasiestática de eventos son muy pequeños. El solucionador explícito es muy eficiente y puede lidiar con el material y las no linealidades de contacto con relativa facilidad porque no se debe formar ninguna matriz de rigidez en cada iteración. Las aceleraciones nodales se pueden resolver directamente.