Contraintes d’optimisation
Découvrez les contraintes d’optimisation et comment les spécifier.
Objectifs de la formation
- Utiliser les contraintes en tant que restrictions de surface
- Observer que des conflits de contraintes peuvent rendre un problème irréalisable
- Rappeler que la mesure de proximité est une valeur qui indique la proximité par rapport à une solution réalisable et comment elle peut être utilisée pour déterminer la faisabilité d’un problème dans un tracé de convergence
À propos des contraintes
Chaque problème d’optimisation constitue une entrée. Dans Grading Optimization, il s’agit d’une surface de terrain naturel composée de triangles. Le solveur d’optimisation modifie la surface et, une fois l’opération terminée, renvoie une nouvelle surface. Toutefois, nous ne voulons pas d’une surface aléatoire. Parmi les innombrables surfaces différentes que le solveur peut créer, c’est celle qui répond à des critères spécifiques qui convient. Par exemple, vous pouvez souhaiter que la surface dépasse une pente maximale de 33 % (ou un rapport de 3:1) à n’importe quel point. Les restrictions de ce type sont appelées contraintes.
une contrainte dans Grading Optimization est une restriction placée sur la surface d’entrée.
Faisabilité
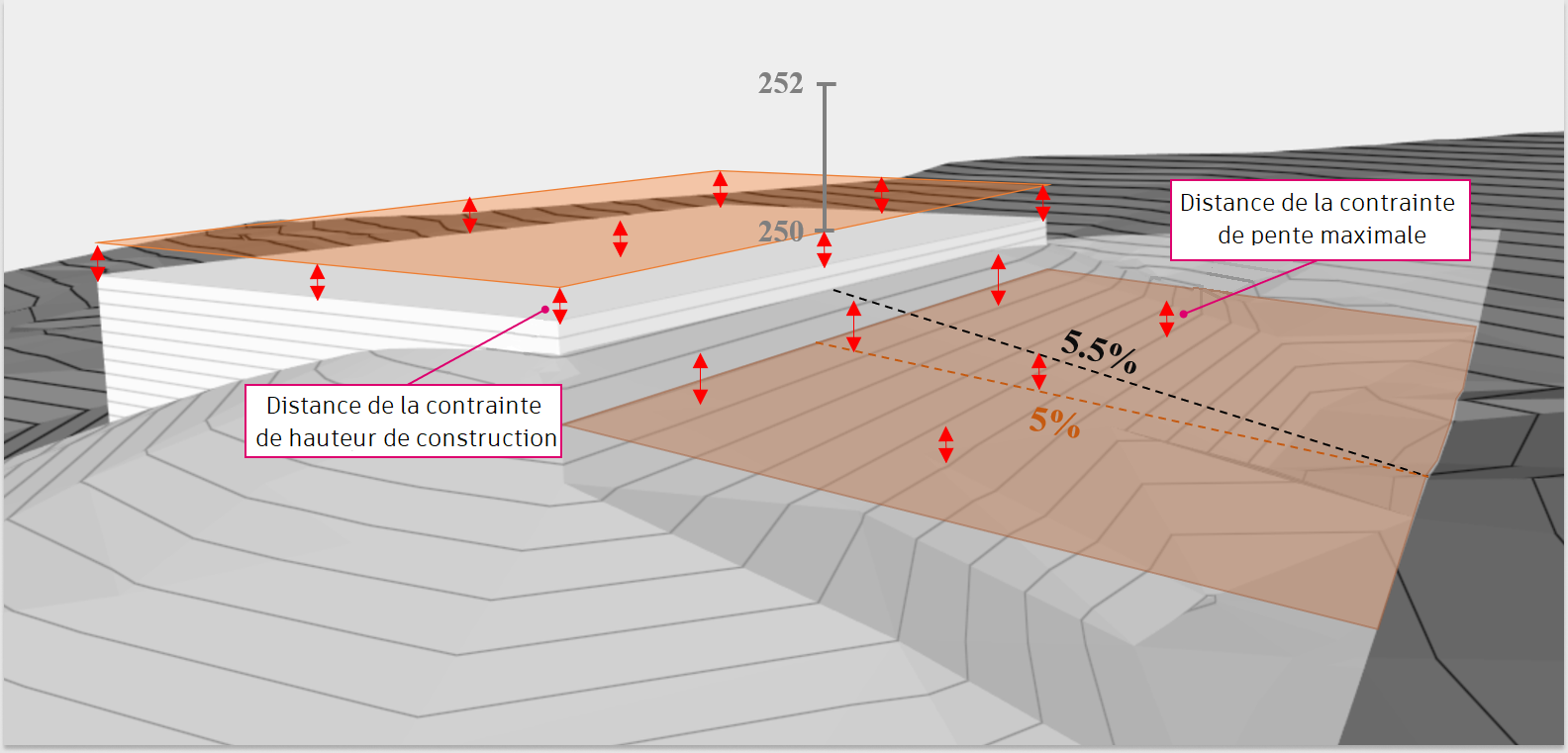
Vous pouvez appliquer un grand nombre de contraintes à une surface. Vous pouvez aussi ajouter une combinaison de contraintes en conflit. Prenons l’exemple du dessin suivant représentant un terre-plein sur un terrain.
Supposez les contraintes suivantes :
- Une contrainte de pente maximale est définie sur 5 %.
- L’élévation du terre-plein est comprise entre 250 et 252 mètres.
- La limite de propriété se termine à 100 mètres du bâtiment.
- L’élévation de la limite de talus est de 244 mètres.
La pente entre la limite de talus et l’élévation minimale du bâtiment est de 6 %, ce qui est supérieur à la pente maximale de 5 % spécifiée. La solution pour le terrassement de cette surface n’est pas réalisable.
Grading Optimization peut malgré tout travailler avec un problème incohérent et trouver une solution raisonnablement réalisable. Dans cet exemple, la solution pourrait résoudre l’endroit où la pente du terrain se termine à 5,5 % et où l’élévation du bâtiment est fixée à 249,5 mètres.
un problème réalisable peut toujours être résolu. Si un problème n’est pas réalisable, Grading Optimization trouvera une approximation optimale.
Proximité
Grading Optimization modifie les élévations de surface de manière itérative pour résoudre les contraintes. Plus il s’approche d’une solution réalisable, moins il est nécessaire d’apporter des changement au niveau de la surface. La quantité de changements nécessaires pour la surface dans une itération, pour respecter chacune des contraintes, est mesurée par une valeur que nous appelons la mesure de proximité.
la mesure de proximité est la somme des distances entre la position des points de surface actuels et la position à laquelle chaque contrainte individuelle les obligerait à se trouver.
Cela est parfaitement illustré dans l’exemple d’approximation précédent. Supposons que la solution est représentée par le dessin suivant.
La distance entre le terre-plein à 249,5 et la contrainte de hauteur à 250 est de 0,5. S’il existe 10 points de terre-plein, chacun d’eux se trouve à une distance de 0,5 de la contrainte de hauteur. La somme de ces points contribue à un total de 10 * 0,5 = 5 par rapport à la valeur de proximité.
En outre, le groupe de points issus des triangles sur le terrain qui sont inclinés à 6 % est également situé à une certaine distance de la surface de pente souhaitée de 5 %. Si nous supposons que la somme de toutes les distances de ce groupe s’élève à 10, alors nous obtenons une mesure de proximité totale de 5 + 10 = 15 pour notre meilleure approximation. Comme le solveur ne peut pas améliorer cette solution, la mesure de proximité restera constante à cette valeur 15, au fur et à mesure que les itérations progressent.
lorsqu’un problème est réalisable, la mesure de proximité diminue vers zéro au fur et à mesure que les itérations progressent. Si un problème n’est pas réalisable, la valeur de proximité se stabilise à une valeur supérieure à zéro.
Dans Grading Optimization, vous pouvez examiner la mesure de proximité dans la partie Faisabilité de la boîte de dialogue Tracés de convergence.
Cliquez sur 
dans l’onglet Violation ou Déblai-Remblai du groupe de fonctions Optimisation pour ouvrir la boîte de dialogue Tracés de convergence.
Les images ci-dessous montrent la mesure de proximité pour quatre problèmes différents. Les deux premiers sont réalisables, les deux suivants ne le sont pas.
| Réalisable ? | Exemple |
|---|---|
| Oui |  |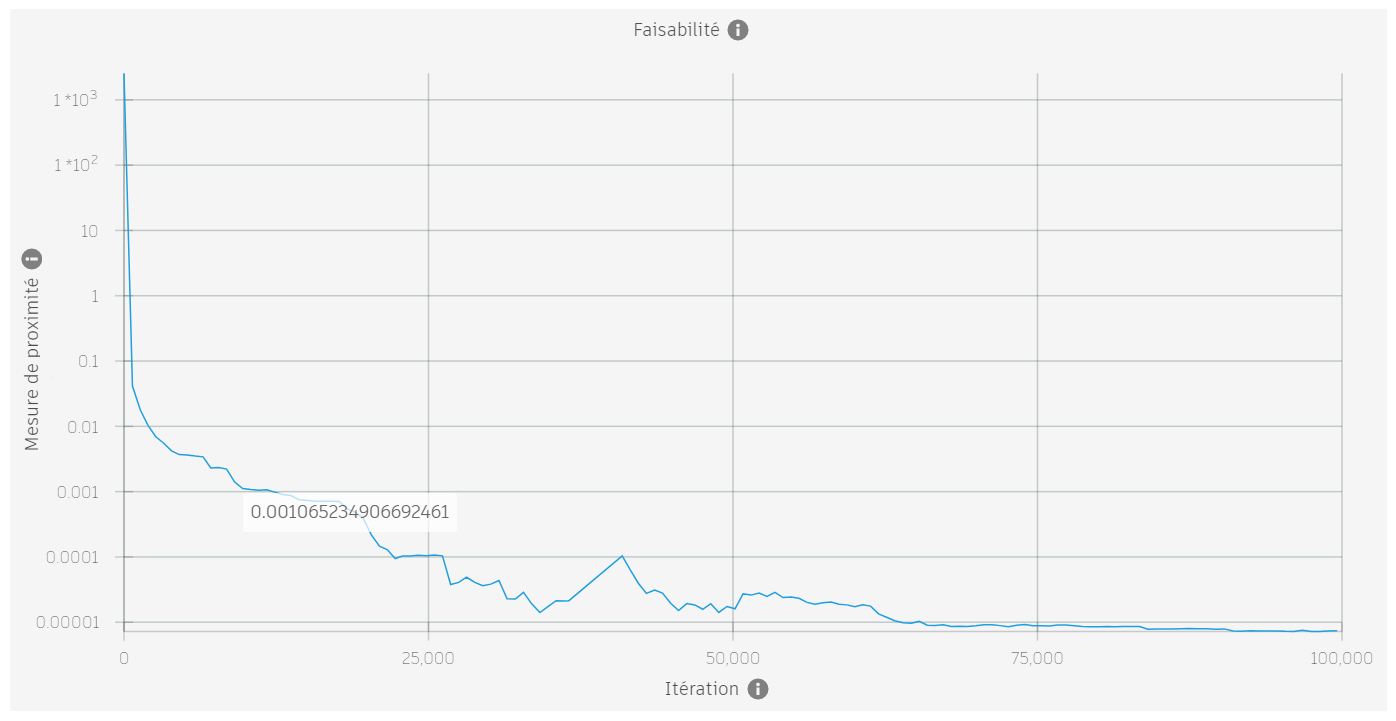
| Oui |  |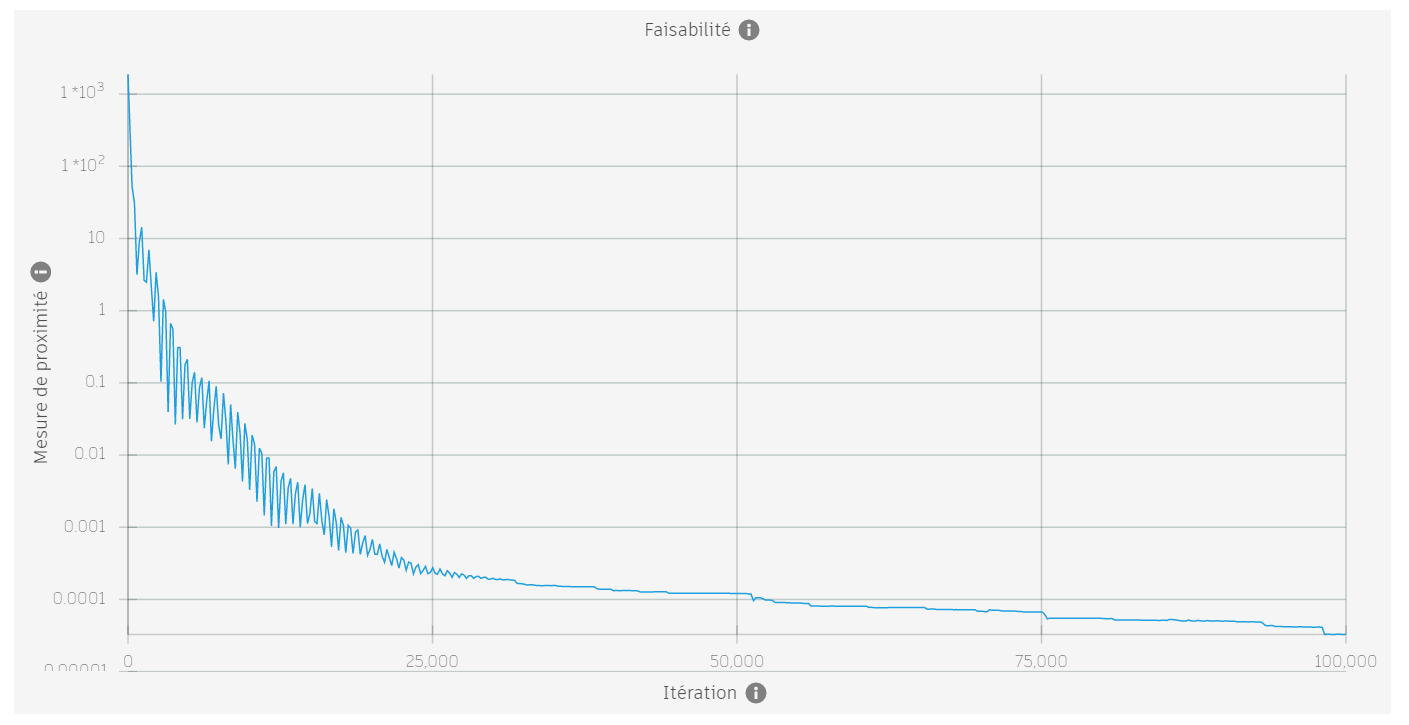
| Non |  |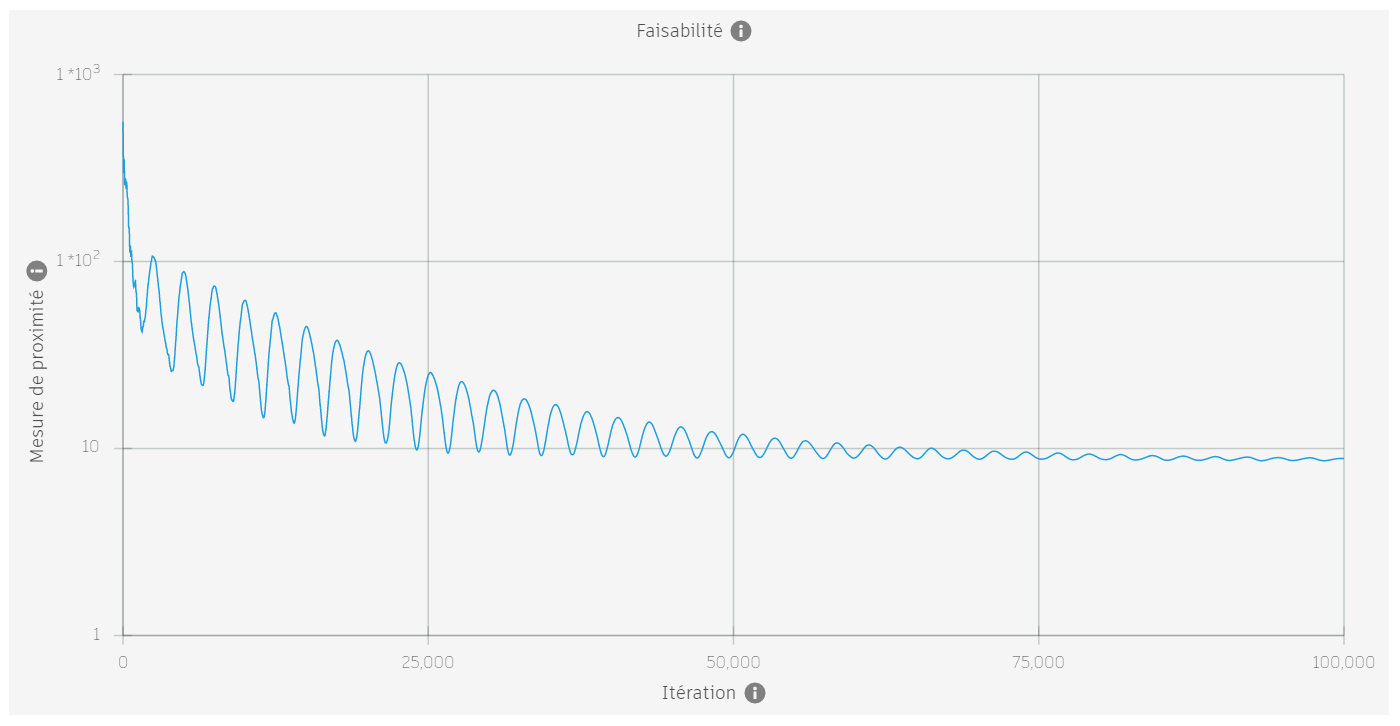
| Non |  |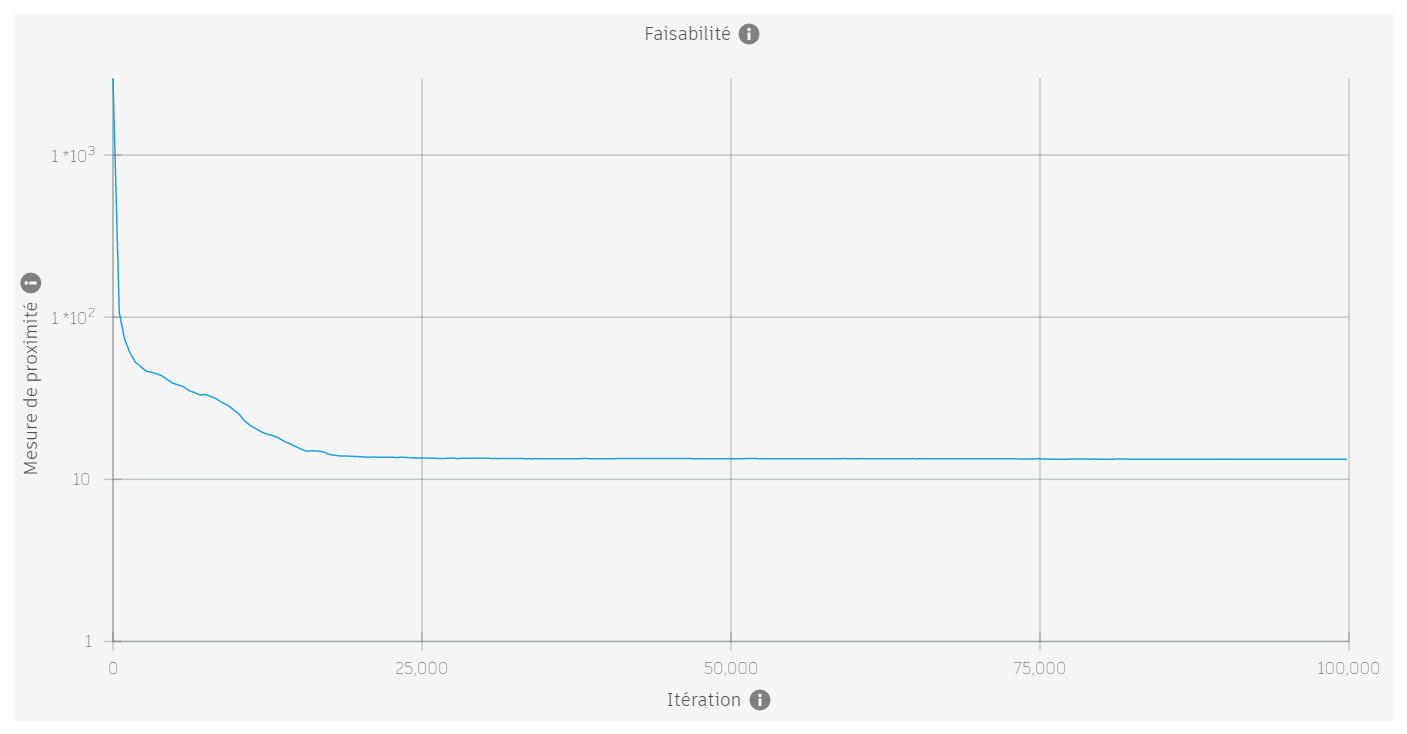
un exemple classique de problème irréalisable se produit lorsque la contrainte de pente maximale sur une zone de limite de talus est définie sur une valeur inférieure aux pentes réelles le long de la limite de talus. Étant donné que les zones de limite de talus ont des limites fixes, le solveur ne sera pas en mesure de satisfaire la pente maximale à ces emplacements. Dans ce cas, Grading Optimization vous avertit au début de l’optimisation. 