Théorie des matériaux hyperélastiques

Les caractéristiques de contrainte/déformation non linéaires des matériaux hyperélastiques, tels que le caoutchouc, sont complexes. Les nombreuses catégories de matériaux disponibles varient considérablement en fonction du comportement. Pour les simulations non linéaires dans Fusion, les matériaux hyperélastiques sont représentés à l’aide du modèle de matériau Mooney-Rivlin standard à 2 constantes. Les coefficients de matériau sont dérivés des données de contrainte/déformation brutes obtenues de façon expérimentale par ajustement de courbe. Ces données peuvent être basées sur différents tests, y compris les exemples de tests de tension/compression suivants :

• Uniaxial (1 et 2)
• Plan
• Equi-biaxial
• Biaxial
• Confiné
• Triaxial
• Volumétrique

La description de ces tests et des données brutes qu'ils produisent dépasse la portée de cette rubrique. Les tests de matériaux sont effectués en labos spécialisés dans le processus et le lissage de courbe doit être effectué en dehors de Fusion. (Le programme ne dispose pas d'une fonctionnalité intégrée permettant d'accepter les données brutes et d'exécuter la fonction d'ajustement de courbe.) Plusieurs programmes sont disponibles pour exécuter la fonction d’ajustement de courbe nécessaire une fois les données brutes obtenues. L’un de ces programmes est HyperFit, disponible dans une version de démonstration gratuite (fonctionnalités limitées) et une version sous licence. Une licence complète est nécessaire pour générer la courbe et les constantes de matériaux résultantes.

Modèle de matériau hyperélastique Mooney-Rivlin

Les matériaux hyperélastiques dans Fusion sont modélisés à l’aide du modèle de matériau Mooney-Rivlin standard à 2 constantes. La formulation presque incompressible est utilisée, de sorte que les termes volumétriques sont inclus dans la fonction d'énergie de déformation. Les effets de la déformation de cisaillement et de la déformation volumique sont séparés.

Fonction d'énergie de déformation générale Mooney-Rivlin

La relation entre l’énergie de déformation, la déformation de cisaillement et la déformation volumique est exprimée dans la fonction de cas générale suivante (applicable aux modèles à 2 constantes et d’ordre supérieure) :

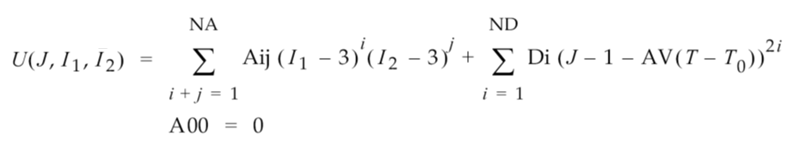
Où :

• U est l’énergie de déformation.
• I1 est le premier invariant de déformation de distorsion.
• I2 est le deuxième invariant de déformation de distorsion.
• J = det F, qui est le déterminant du gradient de déformation.
• Aij est le jeu de constantes de matériaux liées à la déformation de cisaillement (i et j étant les indices des constantes individuelles).
• Di est le jeu de constantes de matériaux liées à la déformation volumique.
• AV est le coefficient volumique de dilatation thermique.
• T est la température actuelle.
• T0 est la température initiale.

Équation de Mooney-Rivlin simplifiée à 2 constantes

Actuellement, Fusion ne prend pas en charge les effets thermiques pour les matériaux hyperélastiques dans les analyses non linéaires. Par conséquent, nous pouvons simplifier la fonction précédente en éliminant les termes de dilatation thermique (AV, T et T0) et en travaillant sur la somme des constantes acceptées par Fusion (A01, A10 et D1). L’équation d’énergie de déformation simplifiée se présente comme suit :

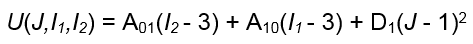
Où :

• *U, J, I1* et I2 sont définis comme précédemment.
• A01 est la première des deux constantes de distorsion liées à la déformation de cisaillement du matériau.
• A10 est la deuxième des deux constantes de distorsion liées à la déformation de cisaillement du matériau.
• D1 est la constante liée à la déformation volumique du matériau, qui est égale à la moitié du module d’élasticité volumique (K).

Autrement dit, 2D1 = K. Par conséquent, D1 = K/2.