Théorie d’analyse de simulations d’événements dynamiques

Ce contexte théorique est vrai pour les simulations d’événements dynamiques et quasi-statiques.

Les simulations d’événements combinent les principes de la loi de Hooke (F=-kx) et de la 2e loi de Newton (F=ma). Après avoir combiné ces deux équations en éliminant le terme de force, nous arrivons à ma + kx = 0. Vous pouvez maintenant ajouter les effets de l'amortissement (F=-cv) pour arriver à l'équation générale du mouvement :

ma+cv+kx = 0

où m désigne la masse, a l'accélération, c le coefficient d'amortissement, v la vitesse, k la rigidité et x le déplacement. Sous forme de matrice, cette équation est représentée par :

[M]{a} + [C]{v}+[K]{x} = 0

À partir de cette équation fondamentale, les contraintes et les déformations peuvent être déterminées à l'aide du vecteur de déplacement {x} et des lois constitutives régissant la réponse du matériau.

Intégration du temps de différence centrale

La simulation d'événements utilise un solveur explicite basé sur l'algorithme d'intégration du temps de différence centrale. Cet algorithme utilise les connaissances des deux états précédents pour résoudre directement l'état actuel (déplacement, vitesse et accélération). La taille du pas de temps d'un état à l'autre est déterminée par l'incrément de temps stable, également appelé limite de stabilité du courant. L'incrément de temps stable régit le plus grand pas de temps autorisé, au-delà duquel la solution va exploser. Lorsque les effets de l’amortissement sont pris en compte, cette valeur est exprimée comme suit :

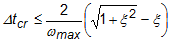
où Δtcr est l’incrément de temps stable, ωmax est la plus grande fréquence propre du maillage et ξ est la fraction de l’amortissement critique dans le mode le plus élevé.

En règle générale, les incréments de temps stables dans une simulation d’événements sont très petits. La bonne nouvelle est que le solveur explicite est très efficace et peut gérer les non-linéarités des matériaux et des contacts avec une relative facilité, car aucune matrice de rigidité ne doit être formée à chaque itération. Les accélérations nodales peuvent être résolues directement.