Arrière-plan théorique des Fréquences modales

Le processus mathématique qui consiste à déterminer les fréquences propres et les formes de mode correspondantes par le biais de l'analyse par éléments finis est complexe. Pour rendre la théorie plus compréhensible, nous allons considérer un système de masse linéaire de ressort très simple avec un degré de liberté. En d’autres termes, la masse peut uniquement se déplacer dans une seule direction.

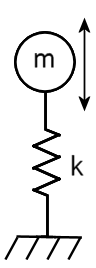
Dans l’image suivante, m est la masse et k est la rigidité du ressort :

schéma du système de masse de ressort avec degré de liberté

La loi de Hooke définit la force (F) requise pour déplacer un ressort de rigidité (k) sur une distance (X) :

(1) F = k·X

La deuxième loi de Newton spécifie la relation entre la force (F), la masse (m) et l’accélération (a) pour le système de degrés de liberté unique :

(2) F = m·a

Si vous combinez ces deux équations, vous obtenez une relation entre la masse (m), l’accélération (a), la rigidité du ressort (k) et le déplacement (X) :

(3) m·a = k·X

L’équation suivante indique la fréquence angulaire d’oscillation (ω), en radians/seconde, pour ce système de masse linéaire de ressort simple :

(4) ω = (k/m)1/2

Il y a 2π radians par cycle de vibration. Par conséquent, l’équation suivante nous donne la fréquence propre d’oscillation (fn), en Hertz :

(5) fn = (k/m)1/2 / (2·π)

Dans un modèle d’éléments finis réel, le mouvement 3D et de nombreux degrés de liberté sont dus à tous les nœuds et éléments du maillage.

Remarque : nous ne prenons pas en compte l'amortissement dans le calcul de la fréquence propre. L'amortissement est défini comme une diminution de l'amplitude de l'oscillation due au fait que l'énergie est retirée du système. L'énergie est perdue en cas de friction, de viscosité ou d'autres forces résistantes. Le degré d'amortissement qui se produit dans les matériaux de fabrication standard (acier, aluminium et béton, par exemple) est faible. La fréquence naturelle sans amortissement n'est donc généralement pas loin de la fréquence naturelle réelle. L'amortissement réduit la fréquence des vibrations par rapport à un système non amorti.

Dans un système continu, il y a un nombre infini de modes vibrants. Cependant, dans un modèle d'éléments finis, il existe un nombre fini de degrés de liberté, et par conséquent un nombre fini de modes propres. La détermination des fréquences de vibration et des formes de mode pour ces systèmes 3D complexes implique des opérations matricielles, des valeurs propres et des vecteurs propres.

L'équation (4) est un problème de valeur propre et de vecteur propre avec un nombre fini de solutions. La fréquence angulaire (ω) est une quantité scalaire. Pour toute solution particulière, tous les degrés de liberté oscillent à la même fréquence angulaire. Toutefois, l'amplitude de la vibration (convient) est une quantité vectorielle. Dans notre système complexe, la ventilation est comparable au déplacement (X) dans notre exemple de degré de liberté unique. Les différents degrés de liberté oscillent avec différentes amplitudes, données par les composants des équipements. Cette variation d'amplitude donne la forme du mode.

La définition correcte des valeurs propres et des vecteurs propres, et les opérations mathématiques utilisées pour résoudre une analyse modale, ne rentrent pas dans le cadre de cette rubrique.