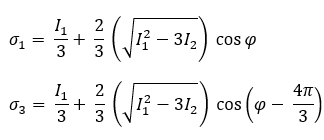Calculs des contraintes principales

Les contraintes peuvent être calculées à partir d’un ensemble d’axes différents des directions X, Y et Z globales. Vous pouvez faire pivoter le système de coordonnées de sorte que seules les contraintes normales restent et que toutes les contraintes de cisaillement soient nulles. Dans cette orientation, le vecteur normal d'une surface et le vecteur de contrainte agissant sur cette surface sont colinéaires. Ensuite, la direction du vecteur normal est appelée direction de la contrainte principale. La magnitude du vecteur de contrainte sur la surface est appelée valeur de la contrainte principale. Il existe trois valeurs de contrainte principales : 1re, 2e et 3e contrainte principale. Ces valeurs sont souvent appelées Maximum, Intermédiaire et Contrainte principale minimale, respectivement.

Les équations mathématiques permettant de déterminer les contraintes principales (σ1 et σ3) sont plus fastidieuses que l’équation de contrainte de von Mises donnée précédemment. Nous devons d’abord déterminer l’angle de rotation (φ), en radians, entre les axes globaux et principaux :

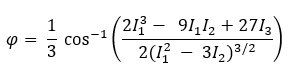
où I1, I2, et I3 sont des invariants de contraintes déterminés par les équations suivantes :

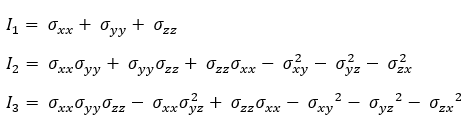
Enfin, les première et troisième contraintes principales sont déterminées par les équations suivantes :