Le caratteristiche di sollecitazione-deformazione non lineare dei materiali iperelastici, come la gomma, sono complesse. I numerosi tipi di materiale disponibili hanno comportamenti molto diversi. Per le simulazioni non lineari in Fusion, i materiali iperelastici vengono rappresentati utilizzando il modello di materiale Mooney-Rivlin standard a 2 costanti. I coefficienti di materiale sono derivati dall'adattamento della curva, ricavati sperimentalmente dai dati di sollecitazione-deformazione grezzi. Questi dati possono essere basati su diversi test, inclusi i seguenti esempi di test di tensione/compressione:

• Uniassiale (1 e 2)
• Piana
• Equi-biassiale
• Biassiale
• Confinato
• Triassiale
• Volumetrico

La descrizione di questi test e dei dati grezzi prodotti non rientra nell'ambito di questo argomento. I test dei materiali sono eseguiti da laboratori specializzati nel processo e l'adattamento delle curve deve essere eseguita esternamente a Fusion. (Il programma non dispone di una struttura integrata che accetta i dati grezzi ed esegue la funzione di adattamento della curva). Sono disponibili diversi programmi per eseguire la funzione di adattamento della curva necessaria dopo aver ottenuto i dati grezzi. Uno di questi programmi è HyperFit, disponibile in una versione demo freeware (con funzionalità limitate) e in una versione con licenza. Per generare la curva e le costanti di materiale risultanti, è necessaria una licenza completa.

Modello di materiale iperelastico Mooney-Rivlin

I materiali iperelastici in Fusion sono modellati utilizzando il modello di materiale Mooney-Rivlin standard a 2 costanti. Viene utilizzata la formulazione quasi incomprimibile, pertanto i termini volumetrici sono inclusi nella funzione di energia della deformazione. Gli effetti della distorsione di taglio e della deformazione volumetrica sono separati.

Funzione generale di energia di deformazione Mooney-Rivlin

La relazione tra l'energia di deformazione, la distorsione di taglio e la deformazione volumetrica è espressa nella seguente funzione di caso generale (applicabile alle condizioni a 2 costanti e di ordine superiore):

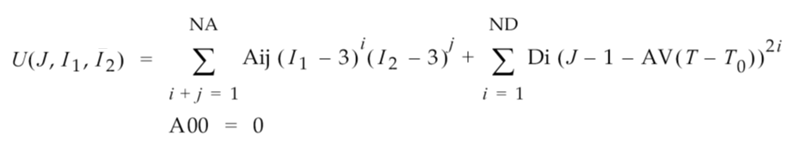
Dove:

• U è l'energia di deformazione.
• I1 è la prima invariante di deformazione di distorsione.
• I2 è la seconda invariante di deformazione di distorsione.
• J = det F è la determinata del gradiente di deformazione.
• Aij è l'insieme di costanti del materiale correlate alla distorsione di taglio (i e j sono i pedici delle singole costanti).
• Di è l'insieme di costanti del materiale correlate alla deformazione volumetrica.
• AV è il coefficiente volumetrico di espansione termica.
• T è la temperatura corrente
• T0 è la temperatura iniziale

Equazione di Mooney-Rivlin a 2 costanti semplificata

Attualmente, Fusion non supporta gli effetti termici per i materiali iperelastici nelle analisi non lineari. Pertanto, è possibile semplificare la precedente funzione eliminando i termini di espansione termica (AV, T e T0) ed eseguendo la somma delle costanti accettate da Fusion (A01, A10 e D1). L'equazione dell'energia di deformazione semplificata diventa quindi la seguente:

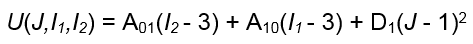
Dove:

• *U, J, I1* e I2 sono definiti in precedenza.
• A01: è la prima di due costanti di distorsione correlate alla deformazione di taglio del materiale.
• A10: è la seconda di due costanti di distorsione correlate alla deformazione di taglio del materiale.
• D1 è la costante correlata alla deformazione volumetrica del materiale, che è uguale alla metà del modulo di compressibilità (K).

Ovvero, 2D1 = K. Di conseguenza, D1 = K/2

Nota Le due costanti di distorsione (A01 e A10) e la costante di deformazione volumetrica (D1) sono i valori definiti dall'utente durante la creazione di un materiale iperelastico nella libreria dei materiali. Questi sono i valori che è necessario ottenere esternamente eseguendo l'adattamento della curva dei dati di test del materiale grezzo. In alcune pubblicazioni, le costanti A01 e A10 sono definite rispettivamente come C01 e C10.