Il processo matematico che consente di determinare le frequenze naturali e le forme di modalità corrispondenti tramite l'analisi ad elementi finiti è complesso. Per facilitare la comprensione della teoria, verrà considerato un sistema massa-molla lineare molto semplice con un grado di libertà (GDL). In altre parole, la massa può spostarsi solo in una direzione.

Nella seguente immagine, m è la massa e k è la rigidità della molla:

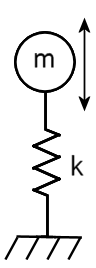
La legge di Hooke definisce la forza (F) richiesta per spostare una molla di rigidità (k) di una distanza (X):

(1) F = k·X

La seconda legge della dinamica di Newton, specifica la relazione tra forza (F), massa (m) e accelerazione (a) per il nostro sistema con GDL singolo:

(2) F = m·a

Combinando queste due equazioni, si ottiene una relazione tra massa (m), accelerazione (a), rigidità della molla (k) e spostamento (X):

(3) m·a = k·X

La seguente equazione fornisce la frequenza angolare di oscillazione (ω), in radianti/secondo, per questo semplice sistema massa-molla lineare:

(4) ω = (k/m)1/2

Per ogni ciclo di vibrazione vi sono 2π radianti. Di conseguenza, la prossima equazione fornisce la frequenza naturale di oscillazione (fn), in Hertz:

(5) fn = (k/m)1/2 / (2·π)

In un modello ad elementi finiti reale, sono presenti movimento 3D e molti gradi di libertà in ragione di tutti i nodi e gli elementi presenti nella mesh.

Nota Nel calcolo della frequenza naturale, non è considerato lo smorzamento. Lo smorzamento è definito come una diminuzione dell'ampiezza di oscillazione dovuta alla dispersione di energia dal sistema. L'energia viene persa nel superamento di forze di attrito, viscose o altre forze resistive. La quantità di smorzamento che si verifica nei materiali di produzione tipici (quali acciaio, alluminio e calcestruzzo) è limitata. Pertanto, la frequenza naturale senza smorzamento non è generalmente lontana dalla frequenza naturale effettiva. Lo smorzamento riduce la frequenza di vibrazione relativa ad un sistema non smorzato.

In un sistema continuo, è presente un numero infinito di modalità di vibrazione. Tuttavia, in un modello ad elementi finiti, è presente un numero limitato di gradi di libertà e, di conseguenza, un numero limitato di modalità di vibrazione. La determinazione delle frequenze di vibrazione e delle forme di modalità per questi sistemi 3D complessi richiede operazioni matrice, autovalori e autovettori.

L'equazione (4) è un problema di autovalore e autovettore con un numero limitato di soluzioni. La frequenza angolare (ω) è una quantità scalare. Per qualsiasi soluzione specifica, tutti i gradi di libertà oscillano alla stessa frequenza angolare. Tuttavia, l'ampiezza della vibrazione (δ) è una quantità vettore. Nel nostro sistema complesso, δ è analogo allo spostamento (X) nel singolo GDL di esempio. I diversi gradi di libertà oscillano con diverse ampiezze, derivanti dai componenti di δ. Questa variazione di ampiezza fornisce la forma di modo.

La corretta definizione di autovalori e autovettori, nonché le operazioni matematiche utilizzate per risolvere un'analisi modale, non rientrano nell'ambito del presente argomento.