Teoria della simulazione evento quasi statica

Questo background teorico è vero per le simulazioni di eventi dinamiche e quasi statiche.

Le simulazioni eventi combinano i principi della legge di Hooke (F=-kx) e della seconda legge di Newton (F=ma). Se si combinano queste due equazioni eliminando il termine forza, si ottiene ma + kx = 0. Ora è possibile aggiungere gli effetti dello smorzamento (F=-cv) per ottenere l'equazione generale del movimento:

ma+cv+kx = 0

dove "m" è la massa, "a" è l'accelerazione, "c" è un coefficiente di smorzamento, "v" è la velocità, "k" è la rigidità e "x" è lo spostamento. Nel formato matrice, questa equazione è rappresentata come segue:

[M]{a} + [C]{v}+[K]{x} = 0

Da questa equazione di base, è possibile determinare sollecitazioni e deformazioni mediante il vettore di spostamento {x} e le leggi costitutive che regolano la risposta del materiale.

Integrazione temporale della differenza centrale

Simulazioni evento utilizzano un risolutore esplicito basato sull'algoritmo di integrazione temporale della differenza centrale. Questo algoritmo utilizza le informazioni di due stati precedenti per risolvere direttamente lo stato corrente (spostamento, velocità e accelerazione). La dimensione del passo da uno stato a quello successivo è determinata dal limite stabilità Courant (incremento passo stabile), che gestisce il passo massimo consentito, oltre il quale la soluzione non andrà a buon fine. Quando si considerano gli effetti dello smorzamento, questo si esprime come segue:

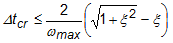
Dove Δtcr è l'incremento passo stabile, ωmax è la frequenza naturale massima nella mesh e ξ è la frazione dello smorzamento critico nella modalità più elevata.

In genere, gli incrementi passo stabili in una simulazione evento quasi statica sono molto piccoli. Il risolutore esplicito è molto efficiente ed è in grado di gestire abbastanza facilmente non linearità di materiale e contatto, poiché non è stato necessario creare alcuna matrice di rigidità per ogni iterazione. Le accelerazioni nodali possono essere risolte direttamente.