準静的イベント シミュレーションの振幅曲線

準静的スタディでは、時間の概念は無次元です。時間は単に、過渡荷重および指定の境界条件の適用を計測する擬似時間です。

荷重値が分かっている場合は、過渡荷重を適用し、[ステップ依存]を有効にして[値曲線]をアクティブにします。

荷重値は分からないが、荷重下での変位が分かっている場合は、指定された拘束により、乗数曲線で指定した手順を使用して、変位の作成に必要な荷重をソルバーに計算させます。

持続時間と振幅

シミュレーションのステップ数を指定し、そのステップにおける過渡荷重(マグニチュード曲線)および強制変位(乗数曲線)境界条件を表す振幅曲線を指定します。

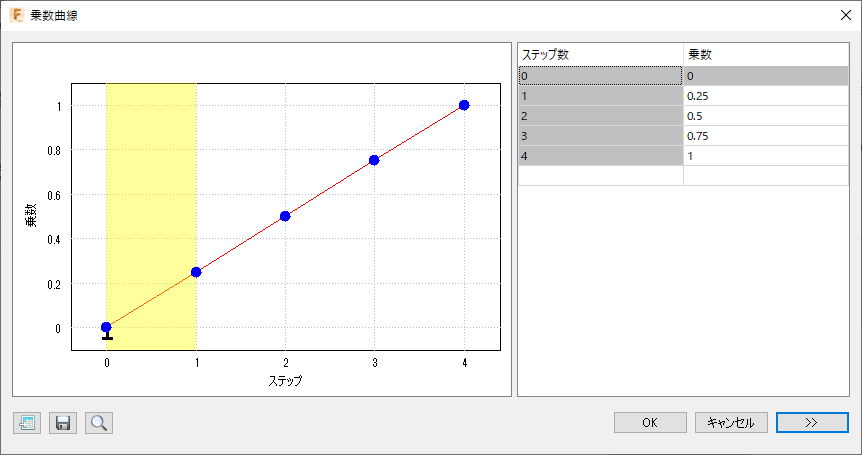
図 1.複数のステップを示す乗数曲線の例。

解析時間に関する考慮事項

既定のステップ数は 1 で、荷重が単調な場合に適しています。この場合、荷重および境界条件をゼロから 1 への線形傾斜で指定します。

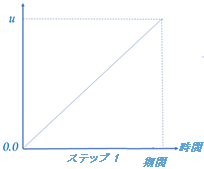
図 2: 線形傾斜が上に向く荷重の問題。

荷重が単調でない場合は、ソルバーが使用するステップ数を指定します。たとえば、指定した値までモデルに荷重を付加してから、荷重を除去してゼロに戻します。このシミュレーションでは 2 つのステップを使用します。

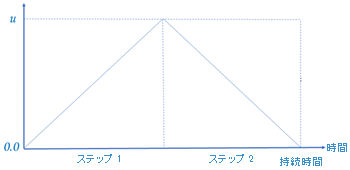
図 3: 線形傾斜が上/下に向く荷重/荷重除去の問題。