異なる変異率での準静的曲線
図 1 に示す 2 つの曲線は、ステップ数が異なり、異なる変位率を定義します。曲線の見かけ上の形状に反して、図 1(a)では、最初のステップで変位率が高くなります。
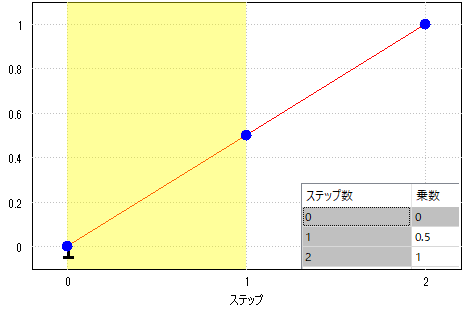
図 1 (a)の曲線は、次の遷移を定義しています。
- ステップ 1 は、完全な変位の 0 から 0.5 の乗数。
一方、図 1 (b)で定義された曲線は、次の遷移を定義しています。
- ステップ 1 は、完全な変位の 0 から 0.25 の乗数。
結果として、ステップ 1 の後で、左側のボディが右側のボディよりも大きくそれています。
 |
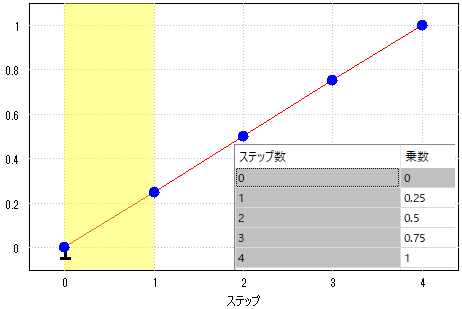 |
| 図 1(a)2 ステップの乗数曲線。実際には、2 番目のステップは 1(b)に一致するように引き延ばされます | 図 1(b) 4 ステップの乗数曲線。この曲線は 1(a)の曲線の形状を制御します |
図 1(a)の曲線は、残りの期間の 0.5 の乗数から完全な変位までの線形のたわみを定義します。
図 1(b)の曲線は、残りの期間における完全なたわみまでの線形移動も定義します。ただし、完全なたわみの 0.25 の乗数から開始します。
両方の曲線が同じ点で終了するため、最初のステップでは左側のボディのたわみが大きくなりますが、後続のたわみの速度は右のボディの方が大きくなるため、同じたわみで同時に終了します。
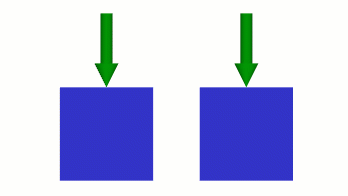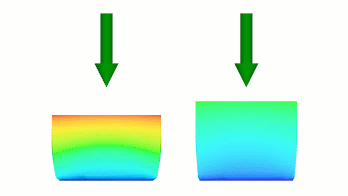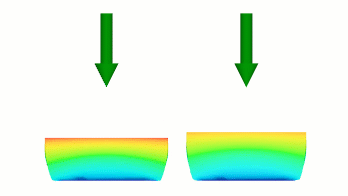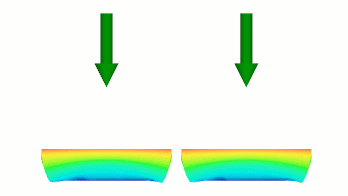 |
図 2 異なる変位率を定義する、異なるステップによる曲線。