超弾性材料の理論

ゴムなどの超弾性材料の応力とひずみの非線形特性は複雑です。利用可能なさまざまなグレードの材料は挙動が大きく異なります。Fusion での非線形シミュレーションの場合、超弾性材料は、2 定数の標準的な Mooney-Rivlin 材料モデルを使用して表されます。材料係数は、カーブ フィットで実験的に取得した応力とひずみの生データから得られます。このデータは、次のような引張/圧縮テストの例を含む、さまざまなテストに基づいている場合があります。

• 単軸(1 と 2)
• 平面
• 等二軸
• 二軸
• 限定
• 三軸
• 体積

これらのテストの説明と生成される生データはこのトピックの範囲外です。材料テストはプロセスに特化したラボで実行し、カーブ フィットは Fusion 以外で実行する必要があります。(このプログラムには、生データを受け入れてカーブ フィット関数を実行するための機能が組み込まれていません。)生データを取得したら、必要なカーブ フィット関数を実行するためにさまざまなプログラムを使用できます。HyperFit はそのようなプログラムの 1 つで、無償のデモ版(一部機能)とライセンス版があります。カーブと結果として得られる材料定数を生成するには、フル ライセンスが必要です。

Mooney-Rivlin 超弾性材料モデル

Fusion で超弾性材料をモデリングするには、2 定数の標準的な Mooney-Rivlin 材料モデルを使用します。ほぼ非圧縮性の定式化が使用されるため、体積条件がひずみエネルギー関数に追加されます。せん断ひずみと体積変形の影響は分けられます。

一般的な Mooney-Rivlin ひずみエネルギー関数

ひずみエネルギー、せん断ひずみ、体積変形の関係は、次の一般的な関数で表されます(2 定数で高次の場合に適用)。

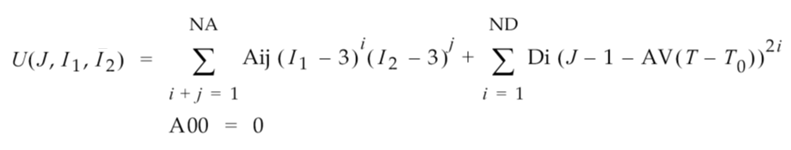
引数の意味:

• U はひずみエネルギーです。
• I1 は 1 番目の変形ひずみ不変量です。
• I2 は 2 番目の変形ひずみ不変量です。
• J = det F は変形グラデーションを決定します。
• Aij はせん断ひずみに関連した一連の材料定数です(i と j は個別の定数の添字です)。
• Di は体積変形に関連した一連の材料定数です。
• AV は熱膨張の体積係数です。
• T は現在の温度です。
• T0 は初期温度です。

2 定数 Mooney-Rivlin 式の簡略化

現在、Fusion は非線形解析で超弾性材料の熱効果をサポートしていません。そのため、熱膨張の条件(AV、T、T0)を削除し、Fusion が受け入れる定数(A01、A10、D1)の合計を計算すると、前述の関数を簡略化できます。簡略化されたひずみエネルギーの式は次のようになります。

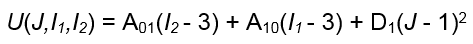
引数の意味:

• *U、J、I1*、および I2 は前に定義したとおりです。
• A01 は、材料のせん断変形に関連する 2 つのひずみ定数の 1 つ目です。
• A10 は、材料のせん断変形に関連する 2 つのひずみ定数の 2 つ目です。
• D1 は材料の体積変形に関する定数で、体積弾性率(K)の半分と等しくなります。

つまり、2D1 = K です。したがって、D1 = K/2 です