モード周波数の理論的背景
固有振動数および、有限要素解析において対応するモード形状を決定する際の数学的処理は、複雑になります。理論を理解しやすくするために、自由度(DOF)を 1 つ含む、非常に単純な直線ばね質量システムについて考えてみます。質量は、1 つの方向に自由に移動できます。
次のイメージでは、m は質量であり、k はばねの剛性です。
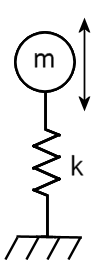
フックの法則では、剛性(k)のばねを距離(X)だけ変位させるために必要な力(F)を定義しています。
(1) F = k·X
モーションに関するニュートンの第二法則では、1 つの自由度のシステムの力(F)、質量(m)、加速度(a)の関係を指定します。
(2) F = m·a
これら 2 つの計算式を結合すると、質量(m)、加速度(a)、ばねの鋼性(k)、および変位(X)の間の関係を次のように表すことができます。
(3) m·a = k·X
次の計算式は、単純な線形ばね質量システムとして、振動運動の角振動数(ω)をラジアン/秒で示します。
(4) ω = (k/m)1/2
振動サイクルごとに 2π ラジアンです。したがって、振動運動の固有振動数(fn)はヘルツ単位で次の計算式のように表されます。
(5) fn = (k/m)1/2 / (2·π)
実際の有限要素モデルでは、メッシュ内の要素とノードのすべてに関わる 3D モーションおよび多くの自由度が存在します。
連続したシステムでは、振動モードの数は無限にあります。しかし、有限要素モデルでは自由度の数は有限であり、振動モードの数も有限です。こうした複雑な 3D システムの振動周波数、およびモード形状を決定する際には、行列操作、固有値と固有ベクトルが必要になります。
計算式(4)は、有限数のソリューションの固有値と固有ベクトルの問題です。角振動数(ω)は、スカラー量です。特定の解析では、すべての自由度が同じ角振動数で振動します。ただし、振動振幅(δ)はベクトル量です。この複雑なシステムでは、δ は、1 つの自由度の変位(X)に似ています。異なる自由度では、δ の成分から得られる、異なる振幅で振動します。この振幅の振動がモード形状に表示されます。
固有値解析を実行するために使用される固有値と固有ベクトルの適切な定義、数学的な操作についてはこのトピックでは触れていません。