モード周波数スタディ
物体はすべて振動をします。私たちにとってなじみの深い、次のような振動源が数多くあります。
- 楽器
- タイヤの車に乗っていてバランスを崩した状態
- 飛行機でパイロットがエンジンを加速したときに生じる揺れ
- 電車が通過したときに足下で感じる振動
振動が長引くと、構造物、車両、およびその他の種類の機械に悪影響を及ぼします。また、振動は避けられない場合が多くあります。振動が止まらない場合、最終的に、金属疲労、パーツの破損、構造物の破損を招く可能性があります。振動は、振動数と関連があります。まさにその本質から、振動には反復運動がともないます。完全な運動シーケンスのそれぞれをサイクルといいます。振動数は、所定の時間内のサイクル数として定義されます。毎秒 1 サイクルは、1 ヘルツと等価です。
構造物の固有振動数は、適用荷重に起因する引張または圧縮応力の影響を受けます。この理由から、Autodesk Fusion には[初期応力を考慮]するオプションが設けられています。このオプションを有効にしていない場合、適用されるモードの効果は無視されます。
モード周波数とは?
構造物に力、加速度、または変形が加えられて励起されると、複数の固有振動数が表れます。特定の固有振動数に対する構造物の運動の仕方のことを、モード形状と呼びます。モード形状には、曲げ、ねじれ、延伸、収縮、またはこれらの効果の組み合わせが伴うことがあります。モード周波数には次に示すいくつかのタイプがあります。
剛体モード: グローバルな軸に関してグローバルな方向または回転で生じる振動運動(特に移動)。これらのモードは、モデルが 1 つまたは複数の方向について拘束されていない場合にのみ発生する可能性があります。モデルは変形せず、元の位置を基準として相対的に移動します。場合によっては、拘束によって、考えうるすべてのモード形状について構造物の振動が防止されます。したがって、拘束のないモデルでモード解析を実行すると便利な場合がありますが、剛体モードは通常は有意義ではありません。
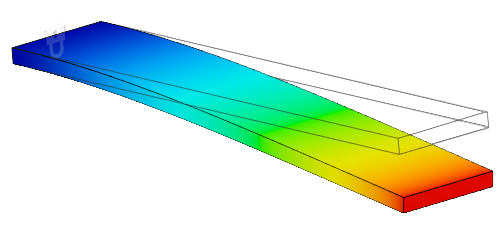
基本モード: 第 1 (最低周波数)モード(剛体モードを除く)。たとえば、誰かが飛込板の端に立っているときの板の形状は、第 1 基本振動モードに類似しています。
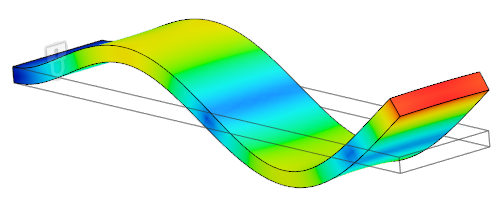
調和モード: 通常は、いずれかの基本モードの倍数。調和モードの形状は基本モードよりも複雑で、より多くのねじれ点があります。先ほどの飛込板の例に戻りますが、基本振動モードの第 2 調和振動の図を次に示します。長さ(濃い青)に沿って 2 つのねじれ点があります(板の固定された端点は数えません)。
1 つのモードについて、単純な上下運動が生じる可能性があります。また、単純な側面から側面への動きや前面から背面への動きが、より高い頻度で生じる場合があります。こうした単純な基本モードの間に、1 つまたは複数の調和振動モードが見つかる場合があります。したがって、連続する(より振動数の高い)モードごとに必ずしも形状の複雑さが増すとは限りません。ただし、全体的な傾向として、振動周波数が高くなると形状の複雑さは増します。
次の係数が、固有振動数やモード形状に影響を与えます。
- 構造物の形状
- 構造物の質量、および質量の分布
- 構造物の拘束方法
- 材料と構造物の剛性
- 構造物に適用される引張または圧縮荷重
たとえば、ピアノ、ギター、またはバイオリンの弦を考えてみましょう。弦の質量が大きくなるほど、その振動周波数は低くなります。逆に、弦の張力が大きくなるほど、その振動周波数は高くなります。最も強い振動は第 1 基本モード(基本周波数)です。基本周波数では、弦全体が単純な円弧の形状で前後に動きます第 1 調和モードでは、弦の形状は S 字状になります。つまり、長さの中間点にねじれ点が 1 つあり、弦の半分の部分が反対方向に移動します。低い周波数モードの上に高い周波数振動が重なると、倍音が生じます。
なぜモード周波数解析を実行するのですか?
モーターなどの動力源によって周波数が生じ、それを振動数として付属の構造物が自然振動を起こした場合、重大な結果が生じる可能性があります。物体が固有振動数で励振されると、振動が増幅されます。この現象のことを共振といいます。パーツが応力に耐えるように設計されていない限り、振動によって物体に共振が起きると、破壊が生じることがあります。
エンジニアは、機械の通常の運転中に共振が起こらないように設計する必要があります。それが、モード周波数の解析の主な目的です。理想的には、第 1 モードの振動数は、他の起こり得る運転振動数より高くなります。または、動作速度での運転周波数が固有振動数を超えることがあります。この場合は、機械が動作速度にまで加速される間に生じる一時的な共振に耐えるような設計が必要になります。
特殊なケースとして、エンジニアが共振を実現する設計を望む場合があります。そうした機器の例として、超音波洗浄器があります。機械の振動に必要な動力を最小限に抑え、振動の大きさを最大にするために、構造物を固有振動数で励起します。
目標が固有振動数の回避であっても実現であっても、モード周波数のシミュレーションは設計プロセスの重要な要素となります。