Teoria da análise da simulação dinâmica de eventos

Esse plano de fundo teórico é verdadeiro para simulações de eventos dinâmicos e quase estáticos.

As simulações de eventos combinam os princípios da Lei de Hooke (F=-kx) e da 2ª Lei de Newton (F=ma). Após combinar essas duas equações ao eliminar o termo força, chegamos a ma + kx = 0. Agora, podemos adicionar os efeitos de amortecimento (F=-cv) para chegar à equação geral de movimento:

ma+cv+kx = 0

onde m é a massa, a é a aceleração, c é um coeficiente de amortecimento, v é a velocidade, k é a rigidez e x é o deslocamento. Em formato de matriz, esta equação é representada como:

[M]{a} + [C]{v}+[K]{x} = 0

A partir desta equação fundamental, as tensões e as tensões podem ser determinadas com o uso do vetor de deslocamento {x} e das leis constitutivas que regem a resposta do material.

Integração do tempo de diferença central

A simulação de eventos usa um solucionador explícito criado com base no algoritmo central de integração de tempo de diferença. Este algoritmo usa o conhecimento de dois estados anteriores para resolver diretamente o estado atual (deslocamento, velocidade e aceleração). O tamanho do intervalo de tempo de um estado para o outro é determinado pelo incremento de tempo estável, também conhecido como Limite de estabilidade do Corante. O incremento de tempo estável determina o maior intervalo de tempo permitido, além do qual a solução explodirá. Quando os efeitos do amortecimento são considerados, isso é expresso como:

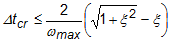
Onde Prectcr é o incremento de tempo estável, ω máx é a maior frequência natural na malha, e ξ é a fração de amortecimento crítico no modo mais alto.

Em termos gerais, os incrementos de tempo estáveis em uma simulação de evento são muito pequenos. A boa notícia é que o solucionador explícito é muito eficiente e pode lidar com material e não linearidades de contato com relativa facilidade porque nenhuma matriz de rigidez precisa ser formada em cada iteração. Acelerações nodais podem ser resolvidas diretamente.