O processo matemático por trás da determinação de frequências naturais e as formas de modo correspondentes por meio da análise de elementos finitos é complexo. Para tornar a teoria mais fácil de entender, consideraremos um sistema linear de massa de molas muito simples com um grau de liberdade (GDL). Isto é, a massa é livre apenas para se mover em uma única direção.

Na imagem a seguir, m é a massa e k é a rigidez da mola:

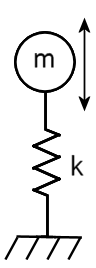
A lei do gancho define a força (F) necessária para deslocar uma mola de rigidez (k) a uma distância (X):

(1) F = k·X

A segunda lei de movimento de Newton especifica a relação entre força (F), massa (m) e aceleração (a) para nosso único sistema de grau de liberdade:

(2) F = m·a

Combinando essas duas equações, temos uma relação entre massa (m), aceleração (a), rigidez da mola (k) e deslocamento (X):

(3) m·a = k·X

A equação a seguir nos fornece a frequência angular de oscilação (Sódio), em radianos/segundo, para este sistema de massa linear de mola simples:

(4) ω = (k/m)1/2

Há dois tempos de birmanês por ciclo de vibração. Portanto, a próxima equação nos fornece a frequência natural de oscilação (fn), em Hertz:

(5) fn = (k/m)1/2 / (2 ・-)

Em um modelo de elemento finito real, temos movimento 3D e muitos graus de liberdade devido a todos os nós e elementos na malha.

Nota: Não consideramos o amortecimento no cálculo de frequência natural. O amortecimento é definido como uma diminuição na amplitude de oscilação devido à energia sendo drenada do sistema. A energia é perdida na superação de forças friccionais, viscosas ou outras resistentes. A quantidade de amortecimento que ocorre em materiais de fabricação típicos (como aço, alumínio e concreto) é pequena. Portanto, a frequência natural sem amortecimento normalmente não está longe da frequência natural real. O amortecimento diminui a frequência de vibração relativa a um sistema não usinado.

Em um sistema contínuo, há um número infinito de modos de vibração. No entanto, em um modelo de elemento finito, há um número finito de graus de liberdade e, portanto, um número finito de modos de vibração. Determinar as frequências de vibração e as formas de modo para esses sistemas 3D complexos envolve operações de matriz, valores próprios e vetores próprios.

Equação (4) é um problema de valor próprio e de vetores próprios com um número finito de soluções. A frequência angular () é uma quantidade escalar. Para qualquer solução em particular, todos os graus de liberdade oscilam na mesma frequência angular. No entanto, a amplitude da vibração (Baixo) é uma quantidade de vetores. Em nosso sistema complexo, o crisol é análogo ao deslocamento (X) em nosso único exemplo de grau de liberdade. Os diferentes GDLs oscilam com amplitudes diferentes, dados pelos componentes do crisol. Essa variação de amplitude nos fornece a forma do modo.

A definição adequada de valores próprios e vetores próprios, bem como as operações matemáticas utilizadas para resolver uma análise modal, estão fora do escopo deste tópico.