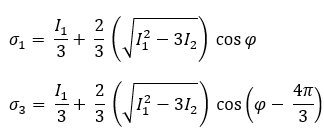Cálculos de tensão principal

As tensões podem ser calculadas com base em um conjunto de eixos que diferem das direções X, Y e Z globais. Podemos rotacionar o sistema de coordenadas para que somente as tensões normais permaneçam e todas as tensões de cisalhamento sejam zero. Nesta orientação, o vetor normal de uma superfície e o vetor de tensão que atuam nessa superfície são colineares. A seguir, a direção do vetor normal é chamada de direção de tensão principal. A magnitude do vetor de tensão na superfície recebe o nome de valor de tensão principal. Existem três valores de tensão principais: 1º, 2º e 3º Tensão Principal. Esses valores são geralmente chamados de Máximo, Intermediário e Tensão principal mínima, respectivamente.

As equações matemáticas para determinar as tensões principais (1 e3) são mais tediosas que a equação de tensão de von Mises anteriormente fornecida. Primeiro, devemos determinar o ângulo de rotação (matemático), em radianos, entre os eixos global e principal:

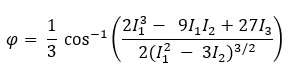
onde I1, I2, e I3 são invariantes de tensão determinados pelas seguintes equações:

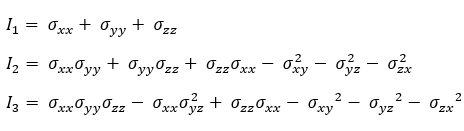
Finalmente, a primeira e a terceira tensões principais são determinadas pelas seguintes equações: