Teoria de simulação de eventos quase estáticos

Esse plano de fundo teórico é verdadeiro para simulações de eventos dinâmicos e quase estáticos.

As simulações de eventos combinam os princípios da Lei de Hooke (F=-kx) e da 2ª Lei de Newton (F=ma). Após combinar essas duas equações ao eliminar o termo força, chegamos a ma + kx = 0. Agora, podemos adicionar os efeitos de amortecimento (F=-cv) para chegar à equação geral de movimento:

ma+cv+kx = 0

onde m é a massa, a é a aceleração, c é um coeficiente de amortecimento, v é a velocidade, k é a rigidez e x é o deslocamento. Em formato de matriz, esta equação é representada como:

[M]{a} + [C]{v}+[K]{x} = 0

A partir desta equação fundamental, as tensões e as tensões podem ser determinadas com o uso do vetor de deslocamento {x} e das leis constitutivas que regem a resposta do material.

Integração do tempo de diferença central

As simulações de eventos usam um solucionador explícito criado com base no algoritmo central de integração de tempo de diferença. Este algoritmo usa o conhecimento de dois estados anteriores para resolver diretamente o estado atual (deslocamento, velocidade e aceleração). O tamanho da etapa de um estado para o outro é determinado pelo limite de estabilidade do Corante (incremento de etapa estável), que governa a maior etapa permitida, além da qual a solução falhará. Quando os efeitos do amortecimento são considerados, isso é expresso como:

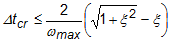
Onde o comando †tcr é o incremento de passo estável, ω máx é a maior frequência natural na malha, e ξ é a fração de amortecimento crítico no modo mais alto.

Em termos gerais, os incrementos de etapas estáveis em uma simulação de eventos quase estáticos são muito pequenos. O solucionador explícito é muito eficiente e pode lidar com material e não linearidades de contato com relativa facilidade, pois nenhuma matriz de rigidez precisa ser formada em cada iteração. Acelerações nodais podem ser resolvidas diretamente.