Prandtl's Membrane Analogy
Imagine a hole cut in a plate, whose shape is the same as that of the cross section for which the torsion constant is required. A homogenous membrane covers the hole and a uniform pressure is applied to the membrane (q per unit area). The membrane deflects into the hole, and at its boundary there is a uniform tension of S per unit length. It can be shown that the deflection z at any point x,y of the membrane is governed by the equation:
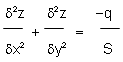
Prandtl introduced the membrane analogy, showing that the torsion in a section is governed by the equation:

where
ϕ is a function of x & y called the stress function
G is the shear modulus
θ is the angle of twist
The analogy can be seen from a comparison of the two equations. The torsion constant of the section is thus derived from the volume under the membrane. For sections which contain one or more voids, the stress function ϕ is constant around the boundary of the void. In the membrane analogy this is equivalent to a horizontal plate with the shape of the void held in position at a certain height above the plate with the hole, so that the membrane just touches the plate all around its perimeter.
A basic understanding of this analogy should assist with the interpretation of results. To appreciate the effect of enclosed voids in a section, imagine a thin cylindrical tube being twisted, and then imagine the same tube with a slit along its length being twisted with the same torque. In the first case the value of the stress function at the void boundary is a positive value, and the torsion constant 'C' is calculated from the volume of the membrane over the whole of the cross section of the tube. In the second case the value of the stress function is zero at all boundaries, and the torsion constant 'C' is calculated from the volume of the membrane over the area of the material of the tube only.
A similar analogy is also applied in the case of shear. In this case the governing equation is:

For shear however the value of the stress function ϕ is not zero at the boundary, and must be calculated for all points around the perimeter of the section.
