2D- und 3D-Splines sind Kurven mit sich ständig änderndem Radius. Inventor unterstützt zwei Arten von Splines und stellt entsprechend für jeden Typ einen Befehl zum Erstellen bereit: Interpolation und Kontrollscheitelpunkt. Nachdem Sie einen Spline erstellt haben, können Sie den Typ über das Kontextmenü ändern.
Interpolationsspline
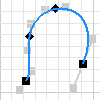
Interpolationssplines verlaufen durch eine Reihe von Punkten, die sogenannten Einpassungspunkte. Damit man sie visuell unterscheiden kann, sind Spline-Endpunkte quadratisch und Spline-Einpassungspunkte entlang der Kurve rautenförmig.
Die Einpassung der Spline-Datenpunkte entlang des Splines legen Sie durch Auswahl der Einpassungsmethode fest:
-
Norm
(Vorgabeeinstellung) oder
Minimale Energie
. Über die in passivem Zustand angezeigten Griffe können Sie die Kurve an jedem Einpassungspunkt formen. Ein 3D-Spline enthält einen tangentialen Griff, verfügt jedoch über keine Steuerelemente für Krümmung und Abflachung. Anmerkung: Der Schieberegler zur Spline-Spannungssteuerung steht für alle Splines zur Verfügung. Mit der automatischen Anpassung der Spline-Spannung wird der Spline in eine Einpassungsmethode Minimale Energie umgewandelt.
- AutoCAD Der Spline verfügt über keine Griffe. Nicht geeignet für die Erstellung von Flächen der Klasse A.
Sie können Spline-Punkte teilweise oder vollständig mit Abhängigkeiten versehen. Die Abhängigkeiten können Sie beim Zeichnen der Kurve durch Ableiten von Abhängigkeiten zu bestehender Geometrie oder durch späteres Hinzufügen von Abhängigkeiten und Bemaßungen erstellen.
Griffe zum Bearbeiten von Splines
Splines, die mit der Einpassungsmethode Norm oder Minimale Energie erstellt wurden, enthalten Bearbeitungsgriffe. Diese tangentialen Griffe befinden sich in passivem Zustand an jedem Einpassungspunkt. Ein passiver Griff hat keine Auswirkung auf die Spline-Form.
Sie können die Spline-Einpassungspunkte bearbeiten oder Bemaßungen hinzufügen, ohne die tangentialen Griffe zu verwenden
Sie können Griffen Abhängigkeiten zuweisen, um Beziehungen mit anderen Geometrien anzugeben.
Kontrollscheitelpunkt-Spline
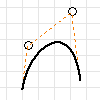
Ein Kontrollscheitelpunkt-Spline wird durch Form- und Lagetoleranzen definiert. Beim Erstellen eines Splines sind die Form- und Lagetoleranzen als Konstruktionslinien zu sehen. Die Spline-Kurven werden durch die als Kreise dargestellten Kontrollscheitelpunkte bestimmt. Die Form eines Splines können Sie durch Verschieben der Kontrollscheitelpunkte anpassen.
Sie können die Endpunkte eines Splines und die Form- und Lagetoleranzen mit Abhängigkeiten und Bemaßungen versehen oder den Spline selbst mit Abhängigkeiten versehen.
Zum Ändern der Spline-Form können Sie die Scheitelpunkte oder die Konstruktionslinien der Form- und Lagetoleranzen ziehen. Das Ergebnis ist meist zuverlässiger als das Ergebnis eines Interpolationssplines, bei dem Einpassungspunkte verwendet werden.
Geometrieversatz von Splines
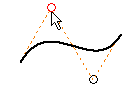
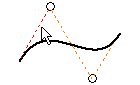
Der Befehl Versatz auf der Registerkarte Skizze dient zum Versetzen einer Geometrie von einer Ellipse bzw. gestutzten Ellipse. Dieses Verfahren eignet sich zur Darstellung einer einheitlichen Hülle.
Bei der Verwendung von Versatz legt der Auswahlpunkt auf der Ellipse den Typ der Versatzgeometrie fest: mathematische Ellipse oder assoziativer Spline mit abstandsgetreuem Versatz von der Ellipse.
Der Befehl Versatz verfügt über zwei Standardeinstellungen, die sich auf das Ergebnis einer versetzten Ellipse auswirken:
- Mit der Konturenauswahl können Sie eine geschlossene Kontur auswählen.
- Mit der Option Versatz beschränken bestimmen Sie einen festen Abstand zwischen der Versatzgeometrie und der ursprünglichen Ellipse.
Krümmung und Glätte von Splines
Die Krümmung ist eine mathematische Angabe des Glättungsfaktors zwischen zwei Kurven oder Flächen. Der Prozentsatz der Richtungsänderung wird als Krümmung bezeichnet. Der Buchstabe G gefolgt von einer Zahl gibt die Glätte der Kurve an.
Die im folgenden Abschnitt beschriebene Kontinuität ist das Ergebnis der Verbindung zweier oder mehrerer Kurven oder Flächen. Abhängigkeiten oder Rundungen glätten den Übergang.
- G0
- Die Endpunkte berühren sich. Der Übergang zwischen zwei Kanten oder Flächen ist erkennbar. Der Übergang kann scharf oder graduell sein
. So verschwindet beispielsweise eine Reflexion auf einer Fläche an der Begrenzung, und eine andere Reflexion erscheint auf der nächsten Fläche. In der folgenden Abbildung einer Zebra-Analyse eines G0-Schnittpunkts zwischen zwei Flächen treffen die Flächen aufeinander. Es ist jedoch keine Rundung vorhanden, die den Übergang glättet. Die Streifen sind nicht angeglichen, und zwischen den Flächen kommt es zu einem abrupten Abriss.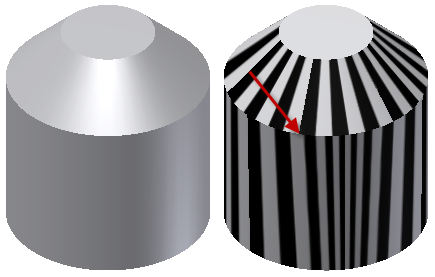
- G1
- Die G1-Kontinuität (Tangente) ist ein glatter Übergang zwischen Kurven. Die beiden Kurven oder Flächen scheinen sich an der Verbindung in dieselbe Richtung zu bewegen, doch die Rate der Krümmungsänderung (Geschwindigkeit) ist erkennbar. So umspannt eine Reflexion beispielsweise zwei Flächen, an der Begrenzung ist jedoch eine Kante sichtbar. In der folgenden Abbildung einer Zebra-Analyse eines G1-Schnittpunkts zwischen zwei Flächen ist zwischen den beiden Flächen eine tangentiale Rundung definiert. Die Streifen treffen aufeinander. Der Übergang zwischen den Flächen ist jedoch scharf und winkelförmig.
- G2
- Die G2-Kontinuität (Krümmung) ist ein glatter Übergang zwischen Kurven. Die beiden Kurven stimmen an den Endpunkten überein, verlaufen tangential zueinander und weisen dieselbe "Geschwindigkeit" (Krümmung) an der Verbindung auf. So erscheint eine Reflexion beispielsweise auf beiden Flächen ohne sichtbare Begrenzung. In der folgenden Abbildung einer Zebra-Analyse eines G2-Schnittpunkts zwischen zwei Flächen ist zwischen den beiden Flächen eine stetige Rundung (G2) definiert. Die Streifen treffen aufeinander, und der Übergang zwischen den Flächen ist glatt und stetig ohne erkennbare Begrenzungen.
- G3
- Die G3-Kontinuität (Krümmung mit konstanter Änderungsrate) ist identisch mit der G2-Kontinuität, jedoch stimmt darüber hinaus die Änderungsrate in den Krümmungen zwischen den Kurven überein. Dieser Übergang ist glatter, ohne erkennbare Begrenzungen. Für Flächen der Klasse A ist G3-Kontinuität oder besser erforderlich. So weist eine Reflexion beispielsweise keine erkennbaren Begrenzungsänderungen zwischen zwei Flächen auf bei hoch glänzendem Finish unter heller Beleuchtung.
Visualisierung der Spline-Krümmung
Die Spline-Krümmung und die Gesamtglättung lassen sich visualisieren. Durch Aktivierung der Option Krümmung anzeigen aktivieren Sie den Krümmungskamm. Dieser veranschaulicht die Krümmung durch eine Reihe verbundener Strahlen, die von der Kurve nach außen weisen. Längere Strahlen zeigen eine stärkere, kürzere Strahlen eine geringere Krümmung an. Die Darstellung der Strahlen kann im Dialogfeld Krümmungseinstellungen angepasst werden.
Die Länge jedes Strahls entspricht der Krümmung des Splines an diesem Punkt, dem Ansichtsmaßstab angepasst. Aus dem Verlauf der Strahlenspitzen lässt sich schließen, wie kontinuierlich die Krümmung des Splines und wie geglättet er ist.