Steady-State Heat Transfer

Multipliers

There are four multipliers that will control the magnitudes of various thermal loads when they are applied to the model. These are located in the Multipliers tab of the Analysis Parameters dialog.

  • The value in the Boundary temperature multiplier field will multiply the magnitudes of any applied temperatures on the model.
  • The value in the Convection multiplier field will multiply the convection coefficients for any convection loads on the model and any surface heat fluxes. (Nodal heat fluxes are not affected by any multiplier.)
  • The value in the Radiation multiplier field will multiply the radiation functions for any surface radiation loads on the model. Body to body radiation is not affected by this multiplier.
  • The value in the Heat generation multiplier field will multiply the magnitudes of any internal heat generation loads on the model.

A value of zero in any of these fields except for the Boundary temperature multiplier field will disable the loads of that type in the model. A value of 0 in the Boundary temperature multiplier field will change the magnitudes of the applied temperatures to 0 degrees.

Default Nodal Temperatures

The value in the Default nodal temperatures field in the Options tab of the Analysis Parameters field will be used to define the temperature of any node that does not have a temperature defined. This should be used if a temperature-dependent material model or radiation is present in the model.

Import Electrostatic Results Joule Heating

If you have previously run an electrostatic current and voltage analysis on a model with identical geometry and mesh to the model that you are currently analyzing, you can apply the electrostatic results to this model to determine the temperature effects of the current. There are a few guidelines that must be followed in this process.

  • You must have run an electrostatic current and voltage analysis. The electrostatic field strength and voltage analysis will not provide the necessary current information.
  • The electrostatic model must be identical in geometry and mesh to the thermal model. The power generation will be applied according to part and element numbers. Therefore, it is important that the models have identical part and element numbering which is dependent on the geometry.
  • You must assign a Heat generation multiplier in the Multipliers tab. This value will be used to scale the heat generation effects of the current.
  • You must apply a heat generation load to the parts for which you want the Joule effects to be calculated. This number is simply a flag that allows you to control the joule effects on a part to part basis.
  • Activate the Use electrostatic results to calculate Joule Effects check box in the Electrical tab of the Analysis Parameters dialog. Specify the electrostatic results file in the Source Model field.

Solver Options

Solution Options Section

The type of solver for a thermal analysis can be selected in the Type of solver drop-down box in the Solution tab of the Analysis Parameters dialog. See also Types of Solvers Available for background information. The options available are as follows:

  • Automatic:. If this option is selected, the processor will choose between the Iterative (AMG) and Sparse options based on the model size. The sparse solver will be the optimum solver for mid-sized models. The iterative solver will be the optimum solver for large models and will require less RAM. If a 64 bit processor is available on the system, the iterative and BCSLIB-EXT solvers will take advantage of it.
  • Sparse: Uses one of the available sparse solvers available in the Type of sparse solver drop-down box. The sparse solvers will use multiple threads/cores when available.
  • Iterative (AMG): Uses an iterative scheme to solve the system of equations. The iterative solver uses multiple threads/cores when available.
  • Iterative PBiCGStab: This option is available for models containing body-to-body radiation or fluid convection. There are two preconditioners available for the solver in the Pre-conditioner drop-down box (see description below).

If for some reason you want to create the solution matrix but not perform the analysis, activate the check box for Stop after stiffness calculations. The only time this would be useful is to access the equation number matrix. The stiffness matrix is always calculated when running an analysis, so there is no advantage to use this option in normal circumstances.

For the sparse and iterative solvers, the Percent memory allocation field controls how much of the available RAM is used to read the element data and to assemble the matrices. A small value is recommended. (When the value is less than or equal to 100%, the available physical memory is used. When the value of this input is greater than 100%, the memory allocation uses available physical and virtual memory.)

As listed above, some of the solvers take advantage of multiple threads/cores available on the computer. The drop-down Number of threads/cores control is enabled in such situations. You want to use all the threads/cores available for the fastest solution, but might choose to use fewer threads/cores if you need some computing power to run other applications at the same time as the analysis.

Iterative Solver General Options Section

If the iterative solver is chosen, then the Iterative Solver section will be enabled. The input for this section is as follows:

  • The Convergence tolerance field will determine how accurate of a solution is found to the matrix of equations. The smaller the tolerance, the more accurate the solution.
  • Maximum number of iterations will stop the analysis if the matrix of equations is not solved within this number of iterations.
    Attention: The accuracy of the solution depends on the convergence tolerance; a smaller tolerance will result in a more accurate solution but may take more iterations. As with any iterative solution, the results should be checked to confirm that they meet the desired accuracy. In some cases, performing the analysis twice with a different convergence tolerance is the best way to confirm the accuracy.

PBiCGStab Options Section

If the Iterative (PBiCGStab) solver is chosen, then the following input will be enabled:

  • The Pre-conditioner drop-down is used to select the method used for the initial guess for the solution of the matrix when the Iterative PBiCGStab solver is chosen. The ILU(0) option is the faster and more efficient option. However, the SSOR option will require less memory. For large models, it may be necessary to use the SSOR option.
  • The Printout interval controls how frequently the status of the Iterative PBiCGStab solver is output. This information can be helpful to monitor the convergence history. For example, a value of 10 would output the convergence status for every tenth iteration of the solver. If the interval is 0, then no status information is printed.

Sparse Solver Section

If the sparse solver is chosen, then the Sparse Solver section will be enabled. The input for this section is as follows:

  • The Type of sparse solver drop-down box contains the sparse solvers currently available. (The sparse solvers are available only for the Windows operating system.) The sparse solvers available are as follows:
    • Default: use BCSLIB-EXT solver.
    • BCSLIB-EXT: use the Boeing solver. The BCSLIB-EXT solver may write temporary files to the folder specified by the environment variable USERPROFILE. By default, this variable is set to the folder C:\Documents and Settings\Username where C: is the drive on which the operating system is installed. The error numbers -701 or -804 returned from the BCSLIB-EXT solver means that it ran out of hard disk space for storing the temporary files. If this occurs, change the USERPROFILE variable to a directory that can provide sufficient hard disk space. (See the Windows Help and Support for documentation on changing environment variables.)
  • The Solver memory allocation field sets the amount of memory to use during the sparse matrix solution for the BCSLIB-EXT solver. In general, allocating more memory should result in a faster analysis. The other sparse solvers adjust the memory setting automatically; so no setting is required for them.

Control Data in Text Output Files

After the analysis is complete, the analysis results can be output to a text file. The Output tab of the Analysis Parameters dialog can be used to control the data that is output to this file.

Control Nonlinear Iterations

If a model contains radiation loads or temperature dependent properties (convection, materials, etc.), the solution will involve a nonlinear iterative process to determine the appropriate temperatures. You can control this process using the Advanced tab of the Analysis Parameters dialog.

If any of the conditions mentioned above exist in your model, activate the Perform check box. You can control how many times the processor can iterate on the solution using the Maximum number of iterations field. The solution after this many iterations will be used as the analysis result. In some cases, an adequate solution will be converged upon before the maximum number of iterations.

There are five options to decide to stop the iterative process. These can be selected in the Criteria drop-down box. If the Do all N iterations option is selected, all the iterations specified in the Maximum number of iterations field will be performed. If the Stop when corrective norm < E1 (case 1)option is selected, the iterations will stop when the corrective norm is less than the value in the Corrective tolerance field. If the Stop when relative norm < E2 (case 2) option is selected, the iterations will stop when the relative norm is less than the value in the Relative tolerance field. If the Stop when either case 1 or 2 option is selected, the iterations will stop when either the corrective norm is less than the value in the Corrective tolerance field or the relative norm is less than the value in the Relative tolerance field. If the Stop when both case 1 and 2 option is selected, the iterations will stop when the corrective norm is less than the value in the Corrective tolerance field and the relative norm is less than the value in the Relative tolerance field.

There are two or four values that are calculated to determine the quality of the convergence. The first value is the corrective norm. The corrective norm is calculated as:

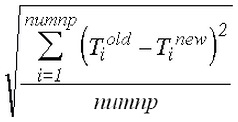
where numnp is the total number of nodes in the model, T old is the temperature from the previous iteration, and T new is the iteration from the current iteration. This norm is related to the temperature difference between iterations; hence the name corrective norm.

The second value for the convergence is the relative norm. This is calculated as:

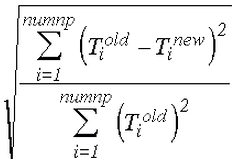
This norm is similar to the relative change in temperature between iterations; hence the name relative norm. The Corrective tolerance field can be used to define the maximum value for the corrective norm. The Relative tolerance field can be used to define the maximum value for the relative norm.

Tip: For the first iteration, the value T old is based on the assigned nodal temperatures (either the default nodal temperature entered on the Analysis Parameters: Options tab or by adding individual nodal temperatures to the model). Thus, you can reduce the number of iterations required to reach convergence if you provide a reasonable initial guess to start the iteration procedure.

When the analysis includes body-to-body radiation, convergence is also based on heat flux (the third and fourth convergence value). The equations for the corrective and relative norms based on heat flux are the same as the above (replacing the temperatures with the heat fluxes).

The temperature of a node after an iteration, T new , could be higher or lower than the final converged value. Thus, you may not want to use this value as the input for the next iteration. The value in the Relaxation parameter field can be used to minimize these oscillations. The relaxation parameter is used as follows:

T cur = T old + (relaxation parameter)*(T new - T old )

In a graphical format, the relationship between the different results can be shown as Figure 1. T cur , and therefore the effect of the relaxation parameter, is the value output to the results file.

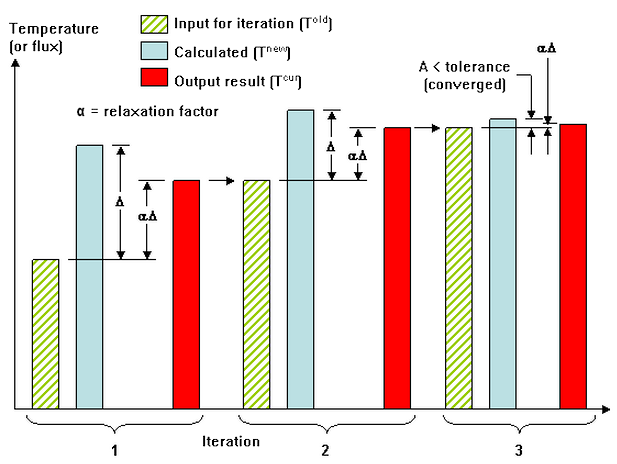
Figure 1: Graphical Interpretation of Relaxation Parameter

A relaxation parameter between 0.8 and 1 will provide good convergence when the nonlinear effects are small. When large nonlinear effects are present such as radiation at high temperatures the relaxation parameter may need to be on the order of 0.1 to 0.3 to smooth the oscillations. The convergence history can be checked in the log file.

Contact Options

There are two methods of handling bonded connections. Which method is used depends in part on whether the nodes are matched between the two parts or not matched.

Activating the option Enable smart bonded/welded contact will use multi-point constraint equations (MPCs) when necessary to bond the nodes on part A, surface B with the nearest nodes on part C, surface D. Shape functions interpolate the temperatures at the nodes on surface B to the nodes on surface D. Therefore, the meshes do not need to match between the parts. The MPCs are used for all the nodes on the surface contact pair whenever any node does not match. If the meshes do match at all nodes, then node matching will be used to bond the contact surface. The two vertices on the adjoining parts are collapsed to one node, and MPC equations are not used for the contacting surfaces. The options for the smart bonding drop-down are as follows:

  • None: Smart bonding will not be used. Therefore, the nodes must match in order for parts to be bonded.
  • Coarse bonded to fine mesh: Smart bonding will create MPC equations that connect the nodes on the surface with the coarser mesh to the nodes on the surface with the finer mesh.
  • Fine bonded to coarse mesh: Smart bonding will create MPC equations that connect the nodes on the surface with the finer mesh to the nodes on the surface with the coarser mesh.

The smart bonding option applies to bonded contact and welded contact. Other types of contact (except for Free) require the nodes to be matched. See the page Meshing Overview: Creating Contact Pairs: Types of Contact for a discussion of defining contact and using smart bonding.

By default, smart bonding uses the condensation method to solve your analysis. If you find your analysis doesn't converge or is not performing as you expect, you can try a different Solution method to use with MPC equations (see Multi-Point Constraints). Click SetupLoadsMulti-Point Constraint and choose from the Solution method options. If you use the Penalty Method, the accuracy of the solution is controlled by the Penalty multiplier field. The Penalty multiplier, times the maximum diagonal stiffness in the model, is used during the penalty solution. A value in the range of 10 4 to 10 6 is recommended.

Note:
  • The solution method you select in the Define Multi-Point Constraints dialog box becomes the method used for all features that include MPCs. These features include, but are not limited to, cyclic symmetry, frictionless constraints, smart bonding, and user-defined MPCs. For example, if you want to use the Penalty Method to solve all your analyses involving smart bonding, you can override the default condensation method by selecting Penalty Method in the Define Multi-Point Constraints dialog box.
  • Smart bonding applied to contact between brick, 2D, and plate elements. Bonded contact involving other element types requires the nodes to match and are not affected by the smart bonding setting.
  • Smart bonding cannot be used when the model includes fluid convection. Reading the velocities from a fluid analysis to cause convection effects in the heat transfer analysis. If a fluid convection load is required, the meshes should match between the parts so that smart bonding is not required.

When the option Enable smart bonded/welded contact is not activated, the parts will be bonded only if the nodes match between the parts.

Parent topic: Analysis Parameters