自由度がきわめて少ない問題では、N 次多項式を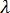 
に与えることで、行列式を明示的に評価できます(N は拘束されていない自由度の数です)。
N 個の実根が存在し、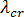 
は単純にこれらの根の中で絶対値が最小のものに等しくなります。座屈方程式に 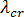を後退代入することで、クリティカル座屈変位モードが得られます。このモードは、座屈で発生する形状変化に対応した一連の変位を任意の倍率で表現したものとして定義されます。したがって、座屈した後の構造の形状を確認するには、変形していない構造の形状に、 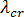に関連付けたクリティカル変位モードを重ね合わせる必要があります。
多数の自由度を持つ構造では、行列式を展開して、根を抽出する方法は実行不可能です。より一般的な解析アルゴリズムを利用するには、一般化した固有値問題として座屈方程式を捉える必要があります。この固有値問題に関連して、N 個の実数の固有値と固有ベクトルのペアが存在します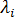 
、 
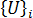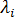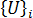。ここで、i = 1,...N です。 また、 および はそれぞれ、 i 番目の固有値と固有ベクトルで、 i 番目のクリティカル荷重係数と座屈変位モードを表します。一般化した固有値問題であれば、それを解くための強力で汎用的な方法がいくつか存在します。ここで使用する方法は、サブスペース反復法と呼ばれるものです [1]。
サブスペース反復法を使用すると、対象の n 個の固有値と固有ベクトルのペアを 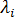の大きさの順に並べた級数が得られます。つまり、次のようになります。
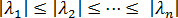。これにより、 =
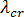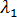および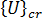 
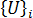= となります 。
取得したい固有値の数は、反り解析や応力解析で指定できるパラメータです。ただし、必要とする固有値と固有ベクトルのペアの解の数が増加すると、計算処理に必要な負荷も著しく増大します。さらに、座屈問題では、「実際の」クリティカル状態のみに関心が向くことが普通で、仮想的な高次のモードは無視されがちです。""頻繁に見られる状況ではありませんが、荷重が増加していく中で、構造が 1 次のクリティカル モードから他の高次のモードに変化する場合(通常は分岐点を通じての変化)、その高次のモードに対応する荷重レベルと座屈形状が、予測した 1 次モードと有意に関連していると見なすことは完全に誤りであり、また危険です。これは、低次から高次の座屈モードに移行している間に構造の形状が大きく変化することが多く、その結果、座屈解析の基本的な前提と明らかに矛盾する状況が生じるためです。
予測した固有値の符号
次の値に制限がないことに注意してください。 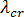には正または負の値も指定できます。したがって、たとえば、
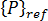を平坦なプレートに引張応力場が形成されるように選択すると、 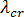は負の値になります。逆に、応力が圧縮状態となるように 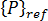の方向を反転すると、 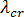は正の値となります。ただし、定義上はいずれの 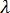の値も正確に同じ絶対値を持ちます。参照荷重 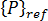が反転可能であれば、1 次の固有値と固有ベクトルのペアのみを得るには実用上、この荷重のみで十分です(これは、 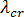が負の値であれば、 の符号が単純に反転するだけであることがわかっているからです )。しかし、反転不可能な荷重系を考える場合は困難が伴います。この場合、座屈は最低次の正の固有値に対応しています。負の固有値の個数を事前に予測することは不可能なので、試行錯誤で進めるか、2 個以上の固有値と固有ベクトルのペアを必要とする単一の解析を実行する必要があります。反転不可能な荷重系(樹脂部品にかかる収縮歪など)を扱った経験則から、最初の 2 つの固有値と固有ベクトルのペアの解で通常は十分であることが示されています。つまり、 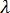の値が、両方とも正の値であるか、一方が正で他方が負であるかのいずれかです。
Sturm シーケンス チェック
サブスペース反復法を使用していると、固有値の欠落が発生することがあります。これは、実際には存在する固有値が、予測された値に取り込まれないためです。この理由から、Sturm シーケンス チェックという手法を使用して、欠落した固有値がないか確認します。ただし、n 個の固有値のいずれかに負の値があると、この手法は機能しません。
座屈結果の有効性
座屈解析を実行するときは、初期の前提がその性質上持っている制限を念頭に置くことが重要です。座屈の前に形状が大きく変化する場合は、有効な範囲を逸脱した条件下でこの手法が適用されることになるので、得られた結果は信頼できないものになります。通常、このことは 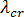が過大評価される結果になりますが、すべての状況でそうなるとは限りません。座屈前の構造の変位量が小さくないと考えられる理由がある場合は、座屈解析に続いて、本格的な大変形解析を必ず実行する必要があります。
座屈のタイプ
-
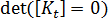
極限点
-
分岐点
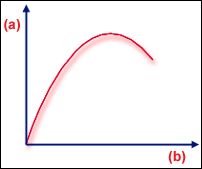
極限点
.(a) 荷重、(b) 変形
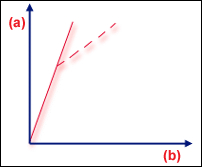
完全な構造の分岐点
.(a) 荷重、(b) 変形
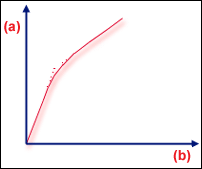
実際の構造の分岐点
.(a) 荷重、(b) 変形
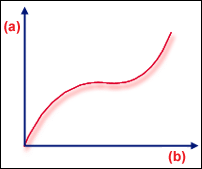
軟化後に硬化
.(a) 荷重、(b) 変形
極限点とは、簡単にいうと、これ以上の荷重を加えると部品の形状が大きく変化する状態です(GUID-065E2D92-2B4E-4450-8CF3-767A371CCE17.htm#FIG_8E8E00D024E74D96B307638F66391293)。これは、ドーム形状の部品でよく見られます。このような部品では、中央にかかった荷重によってドームに「スナップスルー(飛び移り座屈)」が発生することがあります。""極限点タイプの座屈では、座屈点に達する前に形状に著しい非線形性が表れるので、より一般的には、座屈は極限点タイプが望ましいといえます。ドームの例では、剛性マトリックスの行列式がゼロになる前に、部品がある程度平坦になる必要があります。「スナップスルー」(軽度または重度の場合もある)後も、部品にさらに荷重を加えることができますが、一般的には、予想される荷重が極限点を超えないように部品を設計します。""
分岐点とは、可能な 2 つの平衡状態が互いに接する「枝分かれ」点です。""完璧に対称な平坦プレートを考えると、平面内圧縮荷重に対するこのプレートの応答は単純な線形となります。しかし、クリティカル値を超える荷重がかかると、平衡状態は不安定になります。これはたとえば、丘陵形状の頂上に置かれたボールのように、どちら側に転がり落ちるかわからない状態です。したがって、実際の平坦プレートでは、このクリティカル荷重レベルで座屈が発生します。このように、考えられる平衡経路は 2 つあり、その交点を「分岐点」といいます(GUID-065E2D92-2B4E-4450-8CF3-767A371CCE17.htm#FIG_5D265CECEBA9443783273002C74E6C0D)。""
反り荷重問題や温度荷重問題では、これら両方のタイプの座屈が現れることもありますが、一般に多く見られるのは分岐点タイプです。平坦プレートの例では、プレートの不完全性により、分岐点で発生する剛性の急激な変化がはっきりしなくなります(GUID-065E2D92-2B4E-4450-8CF3-767A371CCE17.htm#FIG_4E53D06197A342F49024EDB4A75BF2C0)。他の一般的な反応として、「軟化に続いて発生する硬化」があります(GUID-065E2D92-2B4E-4450-8CF3-767A371CCE17.htm#FIG_8A331E70626C4AE6AEADA8D8552CFE99)。""この場合、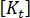 
の行列式は小さい値になりますが、ゼロにはなりません。
GUID-065E2D92-2B4E-4450-8CF3-767A371CCE17.htm#FIG_5D265CECEBA9443783273002C74E6C0D、および GUID-065E2D92-2B4E-4450-8CF3-767A371CCE17.htm#FIG_4E53D06197A342F49024EDB4A75BF2C0 の場合のような座屈解析では、通常、分岐点の位置が明確です。GUID-065E2D92-2B4E-4450-8CF3-767A371CCE17.htm#FIG_8E8E00D024E74D96B307638F66391293 のような場合の解析では、極限点が過大予測される傾向があります。GUID-065E2D92-2B4E-4450-8CF3-767A371CCE17.htm#FIG_8A331E70626C4AE6AEADA8D8552CFE99 のような問題では、明確な座屈荷重がわかりませんが、座屈解析を実行すると、非線形性が現れ始めて条件が厳しくなる点が判明する場合もあります。
参考資料
1. Bathe, K.J., Finite Element Procedures in Engineering Analysis, Prentice-Hall, Englewood Cliffs, New Jersey, 1982, pp. 666-696.