構造の応答をたどる本格的な非線形増分/反復法は汎用性が高い上、比較的高い精度が得られますが、演算処理で大きな負荷が発生します。
座屈の基本的な重要性と設計への導入を考慮すると、座屈の発生が予想されるクリティカル荷重レベルを近似的に求める簡易法には、明確な存在価値があります。座屈発生前の応答が線形で、座屈発生前の変位による影響を無視できると見なせば、このような方法を構築できることが判明しています。座屈解析というこの方法は、初期安定性解析や古典的分岐解析とも呼ばれます。
ここでは、一般化した座屈解析法、および解析で使用する 2 つの具体的な方法について説明します。
一般化した座屈解析
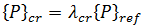
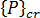 は加荷重分布のクリティカル レベル
は加荷重分布のクリティカル レベル 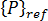 は同じ荷重分布の任意のレベル(参照荷重)
は同じ荷重分布の任意のレベル(参照荷重) 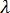 はスカラー乗数
はスカラー乗数
これらの定義では、座屈は、荷重乗数 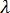 がクリティカル値
がクリティカル値 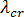 に達したときに発生します。座屈解析は、剛性マトリックス
に達したときに発生します。座屈解析は、剛性マトリックス 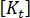 の各係数が、加えた荷重に対して線形に変化すると見なすところから始まります。上記の説明にあるとおり、加えた荷重は、何らかのパラメータ(
の各係数が、加えた荷重に対して線形に変化すると見なすところから始まります。上記の説明にあるとおり、加えた荷重は、何らかのパラメータ( 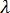 など)に力の定数ベクトル
など)に力の定数ベクトル 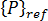 を乗じたものと考えることができます。
を乗じたものと考えることができます。
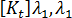 および
および 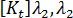 )、および線形性についての前提条件を与えることで、所定の平衡形状
)、および線形性についての前提条件を与えることで、所定の平衡形状 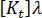 での剛性マットリックスは次のようになります。
での剛性マットリックスは次のようになります。 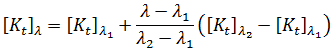
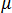 を
を 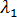 から
から 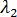 への剛性の変化分を
への剛性の変化分を 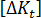 とすると、この式は次のようになります。
とすると、この式は次のようになります。 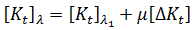
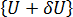 が存在し、両方とも同じ荷重レベルにあります。
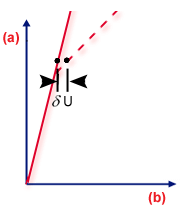
が存在し、両方とも同じ荷重レベルにあります。 これを以下に図示します。ここでは、この平衡形状を 2 つの基本的な座屈タイプ (以降で詳しく説明します) について示しています。
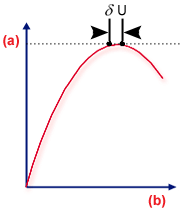
極限点
.(a) 荷重、(b) 変位量
分岐点
.(a) 荷重、(b) 変位量
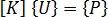 を使用すると、以下の記述が可能です。
を使用すると、以下の記述が可能です。 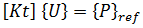
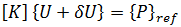
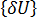 は 2 つの平衡形状間の微小な変位です。2 番目の式から 1 番目の式を減じると、次の式が得られます。
は 2 つの平衡形状間の微小な変位です。2 番目の式から 1 番目の式を減じると、次の式が得られます。 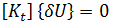
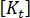 は
は 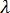 の関数です。線形代数によれば、上記の式を解くことは、次の式を解くことと同じです。
の関数です。線形代数によれば、上記の式を解くことは、次の式を解くことと同じです。 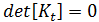
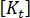 の行列式がゼロになったときに座屈が発生します。一般化した座屈問題で解く式は次のようになります。 これは、 を求める未知数とする固有値問題です。この式は、サブスペース反復法などの標準的な方法で解くことができます。
の行列式がゼロになったときに座屈が発生します。一般化した座屈問題で解く式は次のようになります。 これは、 を求める未知数とする固有値問題です。この式は、サブスペース反復法などの標準的な方法で解くことができます。 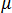 を書き替えると、以下のようになります。
を書き替えると、以下のようになります。 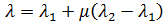
線形(古典的)座屈解析
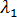 = 0 および
= 0 および 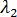 = 1 とします。つまり、ゼロ荷重および全荷重を基準状態とします。この場合、
= 1 とします。つまり、ゼロ荷重および全荷重を基準状態とします。この場合、 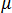 は
は 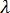 まで小さくなるので、計算式は以下のようになります。
まで小さくなるので、計算式は以下のようになります。 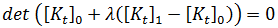
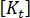 を 2 つの成分に分割できます。
を 2 つの成分に分割できます。 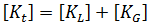
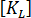 は 1 次剛性マトリックス、
は 1 次剛性マトリックス、 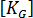 は 2 次以上の剛性マトリックス(応力マトリックス、形状マトリックスとも呼びます)です。
は 2 次以上の剛性マトリックス(応力マトリックス、形状マトリックスとも呼びます)です。 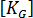 は材料の応力
は材料の応力 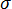 の線形関数です。
の線形関数です。 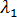 = 0 なので
= 0 なので 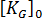 = 0 で、以下のようになります。
= 0 で、以下のようになります。 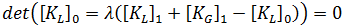
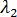 =1 となるまでの応答は純粋に線形であるという点です。 つまり、応力と
=1 となるまでの応答は純粋に線形であるという点です。 つまり、応力と 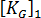 は元の座標を使用して評価します。古典的方法でとっているもう 1 つの前提として、剛性の 1 次部分は荷重によっては変化しないという点があります。つまり、
は元の座標を使用して評価します。古典的方法でとっているもう 1 つの前提として、剛性の 1 次部分は荷重によっては変化しないという点があります。つまり、 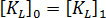 が成り立ちます。トータル ラグランジュ用語法では、これは"変位マトリックス"効果と呼ばれている効果を無視することに相当します。その結果、上記の式は次のように短くなります。
が成り立ちます。トータル ラグランジュ用語法では、これは"変位マトリックス"効果と呼ばれている効果を無視することに相当します。その結果、上記の式は次のように短くなります。 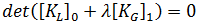
線形座屈法は、反り解析で得られた初期条件に基づかない、構造解析や反り解析で使用します。経験的に、反り問題に古典的座屈解析を使用することで、座屈荷重を正確に予測できることがわかっています。古典的方法が有効に機能するのは、座屈前の形状変化がきわめて少ないからです。つまり、 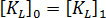 は優れた近似であるということができます。
は優れた近似であるということができます。
線形化座屈解析
この方法では、 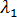 = 0 として、
= 0 として、 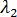 を
を 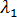 にきわめて近い値とします。つまり、ゼロ荷重およびきわめて小さい荷重を基準状態とします。非常に短いステップをとるので平衡反復は不要で、解析では手法 5 を使用したステップを実行します。
にきわめて近い値とします。つまり、ゼロ荷重およびきわめて小さい荷重を基準状態とします。非常に短いステップをとるので平衡反復は不要で、解析では手法 5 を使用したステップを実行します。
また、 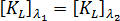 という前提も採用します。この方法では、アップデートした座標を使用して応力を評価します。
という前提も採用します。この方法では、アップデートした座標を使用して応力を評価します。
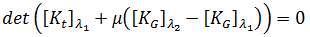
応力を加える前の成分を分析する最も簡単で速い方法は、 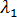 = 0 および
= 0 および 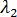 = 0.001 とすることです。したがって、実行が必要なステップは 1 つのみです。また、平衡反復を実行しないので、この解法でのコストは、古典的方法でのコストよりわずかに大きい程度です。
= 0.001 とすることです。したがって、実行が必要なステップは 1 つのみです。また、平衡反復を実行しないので、この解法でのコストは、古典的方法でのコストよりわずかに大きい程度です。
線形化座屈法は、反り解析から得られた初期条件に基づく構造解析のみで使用します。これらの問題ではプロセスによる大きな残留応力が存在するので、古典的方法は適用できません。この状態は、 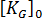 = 0 という前提と矛盾します。このような場合は、代わりに線形化座屈法を使用する必要があります。これは、座屈解析の初期条件を選択するときに [応力] に示されます。
= 0 という前提と矛盾します。このような場合は、代わりに線形化座屈法を使用する必要があります。これは、座屈解析の初期条件を選択するときに [応力] に示されます。