微小変形応力解析(概念)

微小変形解析は最も一般的なタイプの解析であり、大変形解析と座屈解析の両方の基礎となるものです。微小変形解析を十分に理解することは、他のさまざまなタイプの解析を理解するうえで重要な前提条件となります。

微小変形解析は、多くの場合、「線形解析」とも呼ばれます。

仮定

微小変形解析は、柔軟な物体に荷重を加えた結果、発生する変位およびそれに対応する応力と歪が、加えた荷重の大きさと線形の関係にあるという仮定の上に成り立っています。

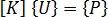
このような線形性を実現するには、この物体の材料が弾性体であり、形状に発生した変化の影響を無視できるくらいに、変位の勾配が物体のどの部分でも十分に小さいと仮定する必要があります。言い換えると、材料面でも形状面でも線形であるかのような挙動を、その物体が示すと仮定することが必要です。つまり、形状に発生した変化によって、構造の剛性が大幅には変化しないということです。このような条件を仮定することで、支配平衡方程式は、次の一般的な形式になります。

ここで、

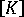は理想構造の全体剛性マトリックス

は未知のノードの変位ベクトル

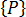は等価なノード荷重のベクトル

構成モデル

線形弾性材料(フックの法則に従う材料)に対する制限の範囲内で、均質材料と非均質材料の両方を扱うことができます。ここではシェル要素(LMT3、LBT3)について、肉厚方向に材料が均質であると仮定します。この制限の範囲内であれば、材料の特性は構造の各点で異なっていてもかまいません。ただし、それら各点には、弾性係数が主要な(最大値と最小値)値となる、直交する 2 つの方向が存在します。これらの方向は直交異方性の方向といい、これに関連付けた材料モデルを直交異方性モデルといいます。

2 つの弾性材料モデルのいずれかを使用できます。1 つは材料に方向性がなく、均質な等方性モデルです。もう 1 つは上記で説明した直交異方性モデルの特殊なもので、主要な係数の場所による違いを無視したモデルです。この場合、材料は複数の方向性を持ちますが、均質です。後者のモデルは、成形プロセスで発生する分子配向の影響を考慮しているので、成形樹脂に適用できます。

境界条件

境界条件を適用する前の平衡方程式は特異行列です。つまり、剛性マトリックス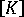は正定値行列ではなく、その逆行列は存在しません。ただし、変位境界条件の適切なセットを適用することで、剛性を正定値で表現することは可能です。考えられるすべての剛体変位モードを排除した場合、得られる短縮化した一連の方程式は、確定的なものになります(つまり、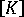は正定値になる)。実際問題として、有限要素モデルに(ピンなどの)内部リリースがなく、その要素自体に擬似的なゼロエネルギモードが存在しなければ、構造が持つ 6 つの可能な剛体運動のそれぞれに対する抵抗が有限値(ゼロより大きい値)となる条件の任意のセットを、変位拘束として設定できます。

利用できる変位拘束の形態を分類するには、拘束ノードにおける自由度ごとの動きが、そのノードと地面との間に取り付けられた外部ばねの抵抗を受けていると想像するとわかりやすくなります。3 つの最も一般的な変位境界条件の形態は次のとおりです。

固定(変位はゼロで、ばねの剛性は無限大)

半固定(変位はゼロではなく、ばねの剛性は有限)

指定 (変位はゼロではない指定値で、ばねが存在しない: 強制変位)

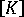固定の拘束は、2 つの方法のいずれかで扱うことができます。その方法の 1 つは、対応する方程式を条件のセット全体から単に削除する方法です。もう 1 つの方法は、必要条件を導く、の対角係数である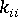を、拘束式をセットの残りの部分から切り離すうえで十分に大きい、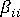などの係数で置き換える方法です。同時に、力のベクトルの i 番目の成分をゼロに設定する必要があります(ベクトルの図: 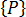)。後者の手法は、 i 番目の成分を以下のように設定するだけで、変位を指定する境界条件にも容易に拡張して適用できます (ベクトルの図: )。

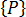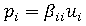
ここで、は必要な変位です。元の方程式全体を維持しておくことの利点は、拘束ノードでの反力の計算に必要な情報を、後退代入の過程で直接利用できることです。

加える荷重

一般化した荷重項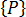は、ノードに直接加えられる集中荷重の他、圧力、牽引力、体積力、初期歪、初期応力などの分散荷重の影響も考慮しているので、等価荷重ベクトルと呼ばれます。分散荷重の場合、ノードの荷重系は指定の分散荷重と必ず平衡状態にあります。単純な要素では、これらの荷重は加えられている荷重と静的に等価です。つまり、静的な平衡条件のみで、荷重の値を知ることができます。しかし、それ以外の場合、荷重の値を知るには、要素の定式に関する詳しい情報が必要になります。あらゆる分散荷重が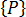に及ぼす影響は解析で自動的に評価されます。

微小変形解析のソリューション

境界条件と加える荷重がわかれば、ノードの変位は次の式から求められます。

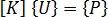
実際問題として、上記の式を解くときに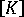の逆行列を作成することは不要であり、非効率的です。代わりに、ガウス消去法でこの式を解きます。

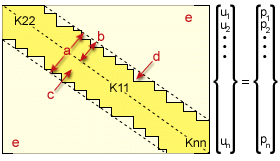
帯剛性マトリックス
.
(a) バンド幅、(b) バンド半幅、(c) プロファイル、(d) スカイライン、(e) バンド外の値はすべてゼロ

剛性マトリックス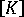は、ガウス消去法の効率を大幅に改善する次の 3 つの特性を持ちます。

このマトリックスは対称マトリックス。つまり、主対角線の一方にあるエントリは、対角線上で反対側の対称位置にあるエントリの「鏡像」。主対角線とは、左上のエントリから右下のエントリに引いた仮想的な線。

このマトリックスにあるほとんどの項の値はゼロ。

このマトリックスでは、ゼロではないすべての項が、主対角線を中心とした狭いバンドの中に存在しています。

GUID-1B128FF9-2E3A-4170-8984-618E66FA4675.htm#FIG_CC0126A4A95B49269FA4E00BEA936191 は、剛性マトリックスの様子を示しています。値がゼロではないほとんどの項と、値がゼロのすべての項の境界は、スカイラインと呼ばれています。主対角線とスカイラインの間に存在する一連の係数をプロファイルといいます。マトリックス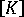は値が帯状にまばらに存在しているので、消去の処理をプロファイルの範囲内に限ることで処理時間が短縮されます。また、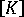の対称性により、計算量がさらに削減されます。これは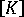の中で消去処理されていない部分は、消去のどの段階でも対称性を維持しているので、対称であることがわかっている項の計算が不要になるからです。

高い効率を得るために、まずノードの再番号付けスキームを使用してプロファイルの中にある係数の数を最小限とします(この再番号付け処理は、ユーザーにはまったく認識できません)。ここで採用されているバンド幅最適化アルゴリズムは、Gibbs、Pool、および Stockmeyer の各氏によるものです [1]。

多くの場合、解析に関与する式の数が膨大となり、仮想メモリ(慣習上、仮想メモリを"コア"と呼んでいます)に係数を格納しきれなくなります。このような大規模な数式を解くには、マトリックス全体を二次ストレージ(普通はハードディスクドライブ)に保存する"コア外"ソルバーを使用します。この場合は、必要に応じてマトリックス全体を複数のブロックに分割し、1 回のガウス消去で処理するのは"コア"に置いた 2 ブロックのみとします(組み合わせの相手となる係数が 2 番目のブロックにあれば、1 番目のブロックは小さくなります)。最小ブロックサイズは、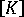のバンド半幅の最大値に等しくなります。最大ブロックサイズは、使用しているマシンに依存しますが、最適な効率を実現するうえで適切な値がプログラムで自動的に割り当てられます(普通は、ブロックサイズを大きくしてブロック数を抑えることで高い効率が得られます)。

複数荷重の場合

応力解析と反り解析には、複数の荷重を指定して解析するためのオプションがあります。これにより、複数の収縮歪が混在する状態や、外部荷重がかかる状態を解析できます。このような複数荷重の場合でも、きわめて効率的に解くことができます。これは、構造の剛性マトリックス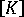が 1 回だけ定式化され、その後は荷重ごとに変位を決定するたびに使用されるからです。それぞれの荷重に対する演算結果は、解析の結果ファイルに書き込まれたジョブ進捗テーブルの 1 行として表示されます。

解析出力

変位場が判明すれば、要素ごとの歪-変位の関係と応力-歪の関係を使用して、要素のさまざまな位置の歪レベルと応力レベルが求められます。FENAS では、要素を体積積分してその要素の剛性マトリックスを求めるときに使用する数値積分位置と一致するように、この歪レベルと応力レベルを求める位置が自動的に選択されます。数値求積位置を応力/歪の回復点として使用することが最適、または最適に近い選択です。

解析出力ファイルには、入力データがそのまま記録されるほか、拘束された変位ノードと初期の変位ノードにおける反力、ノードの変位、および要素の応力が記録されます。

定義上、これらすべての量は加えた荷重と線形の関係にあります。したがって、たとえば荷重が 1/2 になれば、変位と応力も 1/2 になります。これにより、解析結果の定性的有効性を損なわずに、任意の公称強度の荷重を自由に選択できます。ただし、この考え方を拡大して材料係数の影響を扱う場合は注意が必要です。構造に外部荷重がかかっている場合、歪と変位は材料係数と反比例の関係になりますが(直交性材料で比例関係を維持するには、材料係数間の比率を一定に保持する必要があります)、応力は一定のままです。一方、拘束されていない構造に、温度変化や自由収縮などに起因する"内部的"な荷重がかかると、応力は材料の機械的特性と比例関係になります。この場合は、変位が一定のままとなります。内部荷重と外部荷重が混在して加えられる問題では、変位と応力の両方が材料係数に依存するようになります。

結果の解釈

最初の微小変形ソリューションが得られたときに、その結果の妥当性を確認することをお勧めします。確認方法としては、変位場を詳細に調べることが最良です。これは、グラフィカルなポストプロセス機能を使用して容易に実行できます。

ここで確認が必要な内容は以下のとおりです。

パターンは妥当であるか。

概略の大きさは予期したとおりであるか。

予期した対称性が再現されているか。一般的に、このような対称性が再現されるのは、形状、荷重、および境界条件のすべてが対称である場合のみとなる。有限要素のメッシュ自体に対称性がないと、解析結果にどのような対称性が予期されていても、それが正確に再現されることはほとんどない。

一貫性のある変位場が得られ、指定の材料データなどのパラメータとの関係から見て、応力の平均レベルが妥当であることが確認できた後は、より高い精度のメッシュを使用した 2 番目の解析を実行する必要があるかどうかを判断する必要があります。2 種類の異なるメッシュ密度に対するソリューションが必要になる一般的な理由は、単に有限要素法で得られるソリューションは必ず、正確なソリューションまたは完全に収束したソリューションに対する近似であるからです。つまり、精度に対する客観的な尺度は、2 種類のメッシュに対する解析結果に発生した変化に注目することによってのみ得られるということです。

この重要な点をさらに詳しく説明します。応力解析で、フォンミーゼス応力のピークレベルを 95% 以上の精度で予測するために、2 種類のメッシュを使用して、目的の応力の 2 つの値を得たとします。このメッシュの違いによって見られる応力の差が 5% 未満である場合は、この点からの収束が単調であると仮定すると (目的の精度が概略 95～100% の範囲に収まっていれば、一般的にはこのようになります)、細かいほうのメッシュで、目標を超えた精度が得られていることになります。一方、メッシュの違いによる応力差が 5% を超えている場合は、さらに細かいメッシュを使用し、目標の精度が得られるまでこのプロセスを繰り返す必要があります。2 種類のメッシュによるソリューションのみが存在する場合は、細かい方のメッシュでテストを満足していても、粗い方のメッシュでテストを満足するかどうかは判断できません。この判断を下すためには、このメッシュのペアよりも粗い 3 番目のメッシュで解析する必要があります。

以上の背景を踏まえると、細かい 2 番目のメッシュによるソリューションが不要と思われる状況は、実際には 1 つのみであることが明らかです。それは、過去の同様な問題の有限要素解析に基づく豊富な経験により、必要な精度の観点から見て、現在使用しているメッシュで十分な精度が得られることを確信できる場合です。

微小変形解析の妥当性

大変形解析とは対照的に、微小変形解析が効果的なツールである主な理由は、以下の 3 点です。

微小変形解析は、構造の機械的挙動に関する有用で一貫性のある情報を短時間で効率よく取得する方法である。

微小変形解析は、広い範囲の"構造力学"問題に対する理解と見識を築くための優れたツールである。また、微小変形応答をある程度理解していないと、それに対応する大変形応答を理解することが難しい。

微小変形解析は、高コスト効率でメッシュの密度と配分を決定する唯一の手段である。非線形解析は、それぞれ異なる一連の開始条件を設定した線形化ステップの連続と考えることができる。したがって、微小変形収束スタディを基礎として実行する精度チェックは、一般的には、大変形解析でもほとんど同様に有効であると言える。

参考資料

1. Gibbs, N.E., Poole, W.G., and Stockmeyer, P.K., "An algorithm for reducing the bandwidth and profile of a sparse matrix", S.I.A.M. Journal on Numerical Analysis, Vol. 13, No. 2, 1976, pp. 236-250.