構造に荷重を段階的に加えていくと、多くの場合、特定のレベルの荷重で構造の形状がそれまでより急速に変化するようになります。
これは、関連する荷重-変形経路を見ると、グラフの傾きまたは曲率(またはその両方)が明確に変化する部分として容易に判別できます。通常、このような変化は軟化タイプに見られるものです。つまり、グラフの傾きが小さくなり、形状に明らかな変化が現れると共に、それまでよりも急速に変位が増加します。このような挙動を一般的な用語として、座屈と呼んでいます。座屈は、完全な構造の座屈と不完全な構造の座屈という 2 つの主要なタイプに分類できます。
完全な構造の座屈
荷重が増加していくと、完全な構造は最初は GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIG_8464070BF6C6414B8672A81A21BE9588、GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIGURE1B、および GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIG_65E525BE99F2437CB5FE358A531CA4A5 の AB に示す一次(基本)平衡経路に従います。この段階では、剛性が低い方向(横方向または面外方向)に構造の剛性が確実に低下していきます。分岐点と呼ばれる点 B で、抵抗が最小の現在のラインに従って、構造に座屈が発生します。この形態の座屈は、剛性のあるメンブレン(軸)が主体の経路から柔軟性のある曲げが主体の経路への移行が発生したことによって確認できます。細長いビームおよび薄肉のプレートやシェルは、曲げ方向よりも軸方向にはるかに高い剛性を持つので、自ずと最も座屈が発生しやすい形状です。
GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIG_8464070BF6C6414B8672A81A21BE9588、GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIGURE1B、および GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIG_65E525BE99F2437CB5FE358A531CA4A5 の経路 BC は二次または座屈後経路と呼ばれます。分岐点以降の構造の安定性は、B におけるセカンダリ パスの勾配で示されます。B における平衡の状態はそれぞれ、中立(GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIG_8464070BF6C6414B8672A81A21BE9588)、安定(GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIGURE1B)、および不安定(GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIG_65E525BE99F2437CB5FE358A531CA4A5)です。
平衡が不安定な場合は、荷重がわずかに増加しただけでも、構造は、隣接の安定した平衡形状に瞬時に移行します(たとえばGUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIG_65E525BE99F2437CB5FE358A531CA4A5 に鎖線で示した経路 BD)。この現象は、スナップスルー座屈と呼ばれます。GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIG_65E525BE99F2437CB5FE358A531CA4A5 の実線の曲線経路 BCD で示した別の座屈後経路は、スナップスルーが発生しないと仮定した場合に見られる理論的な平衡状態をプロットしたものです。この場合は、点 C で安定な経路に達するまで、荷重が次第に除かれていきます。
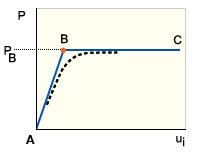
安定性と座屈: 直線状の柱
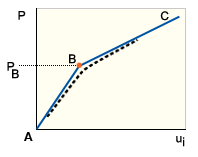
安定性と座屈: 平坦プレート
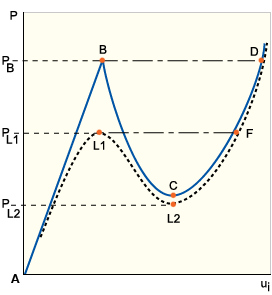
安定性と座屈: 円柱状のシェル
設計者の観点からすれば、安定した座屈後経路が望ましいことは明白ですが、変位が許容可能であれば、座屈後に増加する強度を利用するのはよくあることです。一方、不安定な平衡経路は通常、激しいスナップスルーを伴うため、この経路が許容されることはほとんどありません。さらに、不安定な座屈を示す構造は、多くの場合、構造の不完全性に敏感です。つまり、構造に初期不完全性度と形状のわずかな変化にも、最大荷重容量やクリティカル荷重容量が大きく影響を受けます。
不完全な構造の座屈
実際の構造が完全であることはあり得ません。形状、荷重、境界条件、材料特性のどれにでもわずかな乱れがあれば、真の分岐点が現れなくなることが普通です。プライマリ パスとセカンダリ パスが交差して勾配の不連続点を形成する代わりに、両方のパスが部分的に曲線でつながり、連続した唯一の解が形成されます。結果として見られる座屈後経路は、GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIG_8464070BF6C6414B8672A81A21BE9588、GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIGURE1B、および GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIG_65E525BE99F2437CB5FE358A531CA4A5 に点線で示したラインとなります。不完全性度が低減すると、限られた領域でより大きく変化する曲線になります。完全な構造であれば不安定な分岐点が現れる部分に、不完全な構造では極限点が現れます (GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIG_65E525BE99F2437CB5FE358A531CA4A5 で点 l1)。
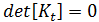
座屈後経路をさらにたどると 2 番目の極限点に行き着きますが、この点は荷重-変位曲線上の最小点に該当します (GUID-3175C968-B186-4A50-954F-CC60B5E1575F.htm#FIG_65E525BE99F2437CB5FE358A531CA4A5 で点 L2)。不安定な状態の経路 L1L2 は、完全な構造での経路と似ていますが、実際には完全には同じではありません。代わりに、鎖線の経路 L1F で示した瞬間的なスナップスルー座屈が発生します。完全な構造の座屈では通常は分岐点が見られますが、実際には必ずしもそうはなりません。座屈前のモード形状に対称性があり、課されている境界条件のためにその対称性が崩れないものであれば、分岐点の代わりに、極限点を経由する不安定な座屈が発生することがあります。このことから、分岐点を伴う座屈は対称性破断と呼ばれることもあります。
解析の考慮事項
対称性を備えた完全な構造について非線形増分解析を実行する場合は、その対称性を崩すために構造にわずかな不完全性を割り当てる必要があります。この処理を行わないと、本来の座屈後経路で座屈が発生せずに、基本平衡経路に沿って継続する解が得られる可能性があります。この現象が発生する可能性がある例として、同軸方向に荷重がかかった直線状の柱や、面内荷重がかかった平坦なプレートがあります。冷却解析結果がない状況で平坦なプレートに反り解析を実行すると、このような面内荷重がかかった平坦なプレートになることがあります。このような場合に推奨できる手順は、目的の座屈モード形状に対応する形状を持つ、形状のわずかな不完全性を構築することです(座屈モード形状が不明な場合は、任意の面外形状を使用できます)。