実際には、ほとんどの構造は、ある制限された範囲の荷重強度に対してのみ、線形またはほぼ線形な応答を示します。荷重が大きくなると、構造の剛性が大幅に変わり、応答が非線形になる可能性があります。
非線形について説明するために、単純ですが現実的なモデルとして、上端に水平方向の力 H と垂直下方向の力 V がかかる、長さ L の細長い柱(下端は固定され、上端は自由)を考えます。先端の下方向への動きを無視すれば、このような荷重系で見られる効果の主体は、柱上端の横方向の変形量となります。ここではこの変形量を u とします。この変位形状の構造と荷重を考慮すると、柱基部にかかる曲げモーメント M が次のようになることは明らかです。
M = HL+Vu
M が、外部荷重の作用であるばかりでなく、u にも依存することから、この問題が非線形であることが直ちに分かります。この曲がった柱に垂直荷重が作用すると、横方向変位がさらに増大することは明らかです。そのため、この問題を直接解くことはできません。ただし、かけられた荷重 H と V を微小な増分に分割して、必要なレベルまで荷重を徐々に増やすことにより、真の解に近づくことができます。
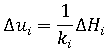
- i は増分の番号
- ki は柱先端の現在の横方向剛性
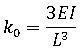
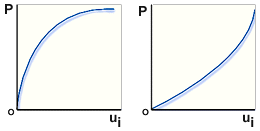
非線形応答に対する荷重 - 変位プロット
.左図 軟化応答、右図 硬化応答、P 非線形荷重、ui 変位プロット
上の例では、非線形の荷重-変形経路に従うという近似方法を使用しました。この方法では、真の応答または精密な応答は、無限に微小なステップをとることによってのみ、求めることができます。非線形応答に関する、より精密なモデルの基本を理解するには、真の荷重 - 変形経路上の各点において、構造が平衡状態になければならない、ということを認識する必要があります。実際には、荷重が増加するにつれて、構造の形状が連続的に変化します。各瞬間の形状は平衡関係によってのみ一意に決まります。このため、荷重 - 変位空間に描かれる曲線は、より正確には、平衡経路と呼ばれます。自由度の高い構造では、荷重強度が変化すると、剛性マトリックスのさまざまな係数が、それぞれ異なる速度で変化します。したがって、加えられた荷重に対して異なる変位成分をプロットすることにより得られた平衡経路は、それぞれまったく異なるように見える場合があります。プロットに適した成分を選択することは任意であると思われがちですが、実は必須です。その理由は、完全な(一般化された)非線形応答は、実際には、(N+1)次元の荷重-変位空間におけるサーフェスにつながるからです(ここで、N は、構造の自由な変位自由度の数です)。
平衡方程式
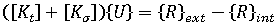
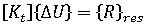
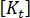 は現在の形状に対する線形剛性マトリックス
は現在の形状に対する線形剛性マトリックス 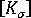 は現在の形状に対する初期応力または形状剛性マトリックス
は現在の形状に対する初期応力または形状剛性マトリックス  は増分節点変位のベクトル
は増分節点変位のベクトル 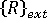 は外部から加わる荷重の現在のレベルに相当する節点力のベクトル
は外部から加わる荷重の現在のレベルに相当する節点力のベクトル 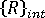 は内部応力場に相当する節点力のベクトル
は内部応力場に相当する節点力のベクトル 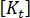 は現在の形状に対する接線剛性マトリックス
は現在の形状に対する接線剛性マトリックス 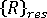 は現在の形状の残差(不平衡な)節点力のベクトル
は現在の形状の残差(不平衡な)節点力のベクトル
これらの方程式は非線形であるため、直接解くことはできません。代わりに、古典的な、反復予測子 - 修正子法 (たとえば、ニュートン法または準ニュートン法) を採用できます。この方法では、左側を予測子、右側を修正子として使用します。通常の(正常に進行する)反復サイクルの間に、構造の形状が真の平衡形状に収束し、同時に、残差不平衡力 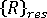 が適宜小さくなります。実際には、(プログラムまたはユーザによって定義された)目標の精度が達成された時点で、反復は終了します。平衡反復中は、荷重レベルが一定に保持されるのが普通です。
が適宜小さくなります。実際には、(プログラムまたはユーザによって定義された)目標の精度が達成された時点で、反復は終了します。平衡反復中は、荷重レベルが一定に保持されるのが普通です。
解法
- KSTRA=0: 初期剛性法
-
非常に負荷が低いですがあまり精密でないこの方法では、初期線形剛性
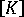 をすべての荷重増分と、1 増分内の各反復サイクルに対して使用します(GUID-319C546E-931F-41D8-805E-130A648F79E8.htm#FIG_4CA25ED1D4EB4624A4923EA6BD146F6C)。変位増分の予測は常に、初期形状に関する剛性マトリックスの線形化に基づいているので、収束するのが非常に遅くなる可能性があり、通常は、平衡経路に無視できない非線形性が発生するとすぐに、アルゴリズムが失敗します(つまり、発散するか、指定された反復回数内に収束できません)。
をすべての荷重増分と、1 増分内の各反復サイクルに対して使用します(GUID-319C546E-931F-41D8-805E-130A648F79E8.htm#FIG_4CA25ED1D4EB4624A4923EA6BD146F6C)。変位増分の予測は常に、初期形状に関する剛性マトリックスの線形化に基づいているので、収束するのが非常に遅くなる可能性があり、通常は、平衡経路に無視できない非線形性が発生するとすぐに、アルゴリズムが失敗します(つまり、発散するか、指定された反復回数内に収束できません)。 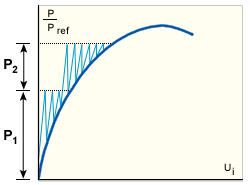
初期剛性法
- KSTRA=1: 修正ニュートン ラフソン法 (MNR)
-
ここでは、各荷重増分の始めに、つまり、前のステップの終わりに得られた平衡形状で、構造剛性マトリックスの更新と因数分解が行われます(GUID-319C546E-931F-41D8-805E-130A648F79E8.htm#FIG_28C732CA09F04500976FFD3A20E1BCF6 および GUID-319C546E-931F-41D8-805E-130A648F79E8.htm#FIG_1BF645306B304487BB8540E9F54C5736)。この場合、剛性を再構成せずに、反復が実行されます。この方法は、平衡経路のうち、非線形性が軽度な部分によく適合します。
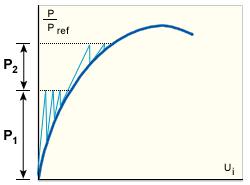
軟化構造に対する修正 NR 法
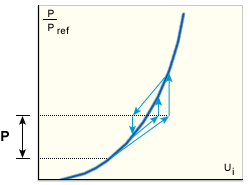
硬化構造に対する修正 NR 法
- KSTRA=2: NR と MNR の組み合わせ
-
これは、MNR 法を修正した方法で、剛性の再構成と因数分解をステップの始めに行い、最初の反復後に再度行います(GUID-319C546E-931F-41D8-805E-130A648F79E8.htm#FIG_BBA0729C970E40F994CC414AB0BCCC08)。このアルゴリズムは、中度の非線形性に対処できます。
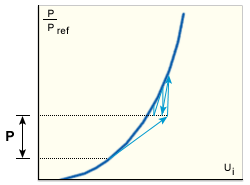
硬化構造に対する組み合わせ法
- KSTRA=3: ニュートン ラフソン法 (NR)
-
この場合は、各反復サイクルの始めに、構造剛性マトリックスが更新されます(GUID-319C546E-931F-41D8-805E-130A648F79E8.htm#FIG_0A62CC011C5E4F39BDEB04521987A31A)。この方法は、速い収束性を示し(つまり 2 次収束する)、平衡経路における強度の非線形性と分岐を処理するのに適しています。ただし、所定の反復回数では、これまでに説明した代替方法の中で、明らかに最も時間がかかります。
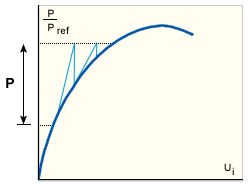
完全 NR 法
- KSTRA=4: ステップ削減したニュートン ラフソン法 (NR)
-
この方法は、KSTRA=3 と同じです。ただし、KSTRA 3 を使用して収束が困難になった場合に、純粋な NR 反復を維持しながら 4 分の 1 のステップ サイズを使用してステップを再実行するために導入されました。
- KSTRA=5: 荷重ステップ法
-
この方法では、一時的に、平衡反復が停止されます。このため、荷重増分ごとに、構造剛性の再構成と削減が 1 回だけ必要になり、反復は使用されません(GUID-319C546E-931F-41D8-805E-130A648F79E8.htm#FIG_919CBE47EC1F4BCF85E632871D4044DF)。真の平衡経路からのずれを最小化するために、荷重増分が MNR や NR で使用されるものよりはるかに小さく、さらに、不平衡力が(処理放棄されるのではなく)次のステップに繰り越される、ということが重要です。この方法は、他のすべての方法が失敗した場合の最後の手段としてのみ使用します。
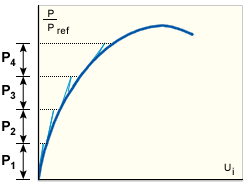
ストレート荷重ステップ法
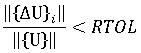
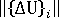 は、2 つの連続的な反復間における、ノード変位の変化に対するユークリッド ノルムです。つまり、以下のようになります。
は、2 つの連続的な反復間における、ノード変位の変化に対するユークリッド ノルムです。つまり、以下のようになります。 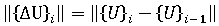
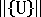 は、現在のノードの総変位に対するユークリッド ノルムです。使用する RTOL の適切な値は、ある程度は問題に依存しますが、値が 0.01~0.0001 の範囲にある場合は、十分な精度が期待できます。
は、現在のノードの総変位に対するユークリッド ノルムです。使用する RTOL の適切な値は、ある程度は問題に依存しますが、値が 0.01~0.0001 の範囲にある場合は、十分な精度が期待できます。 自動制御法
非線形有限要素解析に伴う主な困難点の 1 つは、1 つの反復手法だけでは、解経路全体に対して最適とならないということです。経路の非線形性が厳しくなるほど、選択した手法が収束に失敗し、次の段階に進むことができなくなる可能性があります。ここで明らかに必要となるのが自動制御システムです。このシステムでは、異なるステップ サイズまたは異なる手法を使用して、失敗したステップを再処理することができます。このようなスキームは、解析で利用可能であり、解経路の追跡を、ユーザの介入なしに自動的に行う上で非常に有効であることがわかっています。このスキームの機能は以下のとおりです。
- 初期の最小化手法(通常は KSTRA=1 または 2)および初期のステップ サイズを選択する。この手法は、収束が困難になるまで継続する。
- 次のような場合に、収束が困難と見なされる。
- 許容される最大収束計算回数 max (既定値またはユーザ指定値)内に、収束が得られなかった。
- 解が発散している(発散解と見なされるのは、反復が 4 回以上で、現在の変位増分に対するノルム
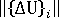 が、ステップの最初の変位増分に対するノルム
が、ステップの最初の変位増分に対するノルム 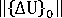 より大きい場合。不平衡力のユークリッド ノルムは、負荷荷重のユークリッド ノルムより大きくなる)。
より大きい場合。不平衡力のユークリッド ノルムは、負荷荷重のユークリッド ノルムより大きくなる)。
- 上記の解法が、KSTRA の値の小さいものから順に並んでいる。収束困難が発生すると、次に序列の高い手法を使用して、ステップが再処理される。同時に、ステップ サイズが、その前の値の 4 分の 1 に縮小される。新しい手法が、次の収束困難が発生するまで継続する。収束困難が発生すると、また次に序列の高い手法が選択され、ステップ サイズが再度縮小される。
- このプロセスは、最大ステップ数に達するか、荷重が許容レベルを超えるまで継続する(これらの両方のパラメータはユーザによって調整可能)。
- 以下のような場合には、最初に選択した手法より序列の高い手法が使用されると、次に序列の低い手法に戻ろうとする。
- 現在の手法 (KSTRA = 1、2、3 または 4) の 4 つのステップが、許容された反復回数の半分以上を必要としなかった。
- 現在の手法 (KSTRA = 5) が 4 回使用された。
序列が低い手法を選択し、それが失敗した場合には、次の 4 つの増分に対して、前の方法が使用されます。ただし、ステップ サイズの縮小は行われません。
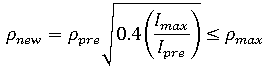
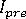 は前のステップで使用した収束計算回数、
は前のステップで使用した収束計算回数、 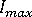 は最大収束計算回数、
は最大収束計算回数、 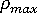 はステップ サイズの限界(ユーザによる調整が可能)です。たとえば、
はステップ サイズの限界(ユーザによる調整が可能)です。たとえば、 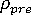 = 1、
= 1、 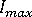 = 20、
= 20、 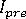 = 4、
= 4、 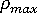 = 2 のようになります。ここで、この式を用いると、現在のステップ サイズが
= 2 のようになります。ここで、この式を用いると、現在のステップ サイズが 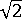 になることがわかります。
になることがわかります。 またこれは、収束の失敗に続いて、平均 4 つの反復で 4 つのステップをそれぞれ処理してから、元のステップ サイズ(失敗した増分で使用されていたステップ サイズ)を復元する、ということを示しています。 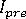 が
が 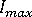 の 40% を超えると、ステップ サイズは比較的ゆっくりですが縮小します。
の 40% を超えると、ステップ サイズは比較的ゆっくりですが縮小します。