構造解析で使用する要素タイプ

Midplane および Dual Domain 解析の構造解析は、シェル要素およびビーム要素どちらでも実行できます。

シェル要素

シェル要素は、エッジが直線で、平面の三角形で構成されます。曲面シェルをモデリングする場合は、シェル要素の"ファセット面"の集合体として表示することにより実際の形状に近づけます。現状では、隣接する要素の厚みが異なる場合でも、各要素の厚みは一定であると仮定しています。

どの場合でも、ノードごとに 6 つの自由度を使用します。これには、グローバルな軸に対して平行な 3 つの並進自由度、およびこれらの軸を中心にした 3 つの回転自由度が含まれます。平滑なシェルの場合には、使用する自由度が 5 つのみの場合もあります。これに含まれるのは、3 つの並進自由度と 2 つの中間サーフェス法線のローカルな回転自由度です。ただし、どの場合でも、6 つの自由度を使用した方が明らかに利点があります。まず第一に、ボックス、トレイ、補剛シェルなどの平滑ではない構造を解析する際に、交差するサーフェス間のジャンクション部に対して特別な拘束を適用する必要がなくなります。第二に、ビーム要素 (3 次元空間では、6 つの自由度が必要です) を、基本となるプレートやシェルのメッシュのノードに、拘束や変換を加えずに直接接続できます。第三に、大変形(幾何学的に非線形な)解析では、3 つの回転自由度を使用することで、有限剛体運動に関して、簡潔で幾何学的に精密なモデルを導入することが可能になります[1-3]。薄肉構造の幾何学的に非線形な既存モデルで不良が発生する場合、原因の多くは、回転パラメータが関係する近似にあります。この解析で使用するパラメータは、関連する回転テンソルのスペクトル解析に直接関係しているという意味で"自然"です。線形化された形式を得るには、オイラーとロドリック[1,3,4]による古典的な剛体運動解析を使用します。

この要素式により、膜変形、曲げ変形、および横せん断変形を処理します。最後のものは、Reissner-Mindlin 理論[5,6]に基づいています。この理論では、横せん断を含めて、 C₁ から C₀ に、連続要件を下げることにより、薄肉プレートとシェルに関する古典的なキルヒホッフの仮説を緩和しています。これにより、"薄肉"および"やや厚肉"の両方の場合のプレートとシェルを、モデル化することができます。実際には、このような要素のパフォーマンスは、プレートやシェルが薄くなるにつれて、急速に低下することがわかっています。この現象は、シアーロッキングと呼ばれており、横せん断歪ゼロという限界条件に要素が適切な二次の割合で近づけないことが原因で発生します。シアーロッキングは、次数低減積分を使用することで緩和されますが、当初の期待に反し[7]、根絶することはできません。最近では、Fried [8]と McNeal [9]により導入したエネルギーバランス法の改良型が、広範囲な構造アスペクト比(シェル構造の中間サーフェスの周囲で測定される特性寸法と、平均肉厚の比率)において優れた成果を挙げています。現在の三角形要素で使用される形式は、Tessler と Hughes [10]によるもので、次のように近似アスペクト比の範囲で高精度な結果を得ることができます。

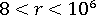
この手法により、ロッキングを除去するだけでなく、要素の歪により薄肉シェルが影響を受けにくくなり、剛性マトリックスのコンディショニングと応力予測の質が向上します。

注: これに類似するメンブレンロッキングの問題は、薄肉曲面要素でのみ発生するので、ここで検討する必要はありません。

現在、モデル化できるのは、線形弾性材料のみです。これらの材料は、等方性または直交性のいずれかです。後者の場合、材料の主平面群に直交性があります。1 つの平面がシェルの中間サーフェスにあると、他の 2 つの平面は 2 つの垂直線(直交異方性の方向と言います)に沿ってこのサーフェスと交差します。直交性方向は、処理によって決まり、充填+保圧解析に基づき、要素ごとに指定されます。各方向の材料特性は、反り解析または応力解析用の解析入力ファイルを準備するときに、ユーザが指定します。

幾何学的な非線形性は、対流ラグランジュ手法に基づいています。この手法では、変位場が、各点でシェルの断面と共回転する、ローカルな対流座標のセットを参照します。整合性を保つため、ここでは、通常の伸張不可能条件を、任意の点で断面ディレクタと共線性があるファイバーに適用します。

共回転手法は、連続体力学の極分解定理から導き出されます。この定理は、一般的な空間運動は、常に、剛体運動に従う純粋な伸び(変形)に分解できるというものです。適切な有限回転測定(上記参照)を選び、全体的な運動から剛体成分をはっきりと切り捨てることで、要素内の内部変形と関連する応力を評価する整合的な方法が実現できます。具体的に、これが意味するものは、剛体運動の大きさに制限を設ける必要がなく、しかも、内部の変形と応力を決定する際の精度が、解析全体を通して一定のままであるということです。

この定式化と密接な関係があるのは、Reissner [11,12]、Simmonds と Danielson [13]、Danielson と Hodges [14]の有限変形理論、さらに Bates [1]および Simo と Vu-Quoc [15]によるこれらの理論における有限要素の導入です。

要素 LMT3

Midplane 解析では、要素 LMT3 を使用します。LMT3 は、3 つのノードからなる、18 自由度 (各ノードごとに 6 自由度) を持つ三角形要素です。この要素を構成するには、Bergan と Nygard [16]および Bergan と Felippa [17]によるローカルな膜の定式化に、Tessler と Hughes [10]による曲げの定式化を重ね合わせ、結合した式をグローバル座標系に適合するように変換します。結果として生成される要素は、膜歪と横せん断歪の双線形変化をモデル化できますが、曲げ歪(曲率)は一定です。

Bergan と Nygard の"自由な定式化"は、仮定変位場に基づいていますが、"不適合な"形状関数の使用を許容することにより、ポテンシャル エネルギーの厳密な定式化からは逸脱しています。確実に収束させるために、あらかじめパッチ テストの要件を適用します。変位形状関数は、基本モードと高次モードに分けられます。基本モードは、剛体と一定の歪状態に関連し、高次モードは、座標不変面内曲げモードに関連します。

これが、基本剛性と高次剛性につながり、それぞれ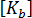 、および 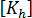で表されます。その結果、合成した膜剛性は、次の形式になります。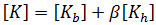

ここで、 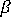は、高次剛性に関する表示倍率となる自由パラメータです。詳細テスト結果に沿って、 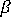= 1.5 が最適な選択として採用されています。

ローカルな中間サーフェス法線回りの回転(通常、面内回転自由度: ドリリング自由度と言います)は、ペナルティ拘束法による中間サーフェスの平均面内回転に関係しています。したがって、次のようになります。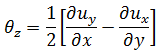

ドリリング自由度は、この定式化では完全に統合されたアクティブな構成要素です。 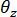と平面内勾配との間の結びつきの強さが、正確に同一平面上にある要素の場合でも残っているので、特異点に関する問題は発生しなくなります。境界条件要素として、 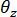を使用する場合は、十分注意を払う必要があります。

この要素の曲げの定式化の基本は、連続横せん断エッジ拘束により実現される、明示的な自由度法です[10]。これを使用することで、側方変位 u_z の双二次変動、および法線回りの回転 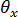、および 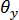の双線形変動を持つ全体的な条件付き(結合)変位場がもたらされます。横せん断補正係数法[10]と組み合わせると、この要素は、広範囲のアスペクト比にわたり、(標準的な一定曲率の定式化に比べて)大幅に向上した曲げ応答を示します。

要素定義

要素に関する、形状、ノード番号、およびローカル/グローバルな自由度を、GUID-C6040A5F-6941-450C-B147-FBC16693CC13.htm#FIG_AF05FFF4B09B4FBABDC03622AC3CD5FE に示します。ノード i、j、k は、解析出力ファイルに示されているノード接続テーブル内のエントリを指しています。たとえば、要素の接続が 11、101、85 の場合、i = 11、j = 101、k =85 となり、ローカル X 軸の方向は、ノード 11 からノード 101 への方向になります。

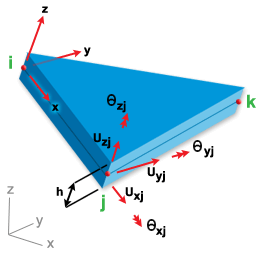
LMT3 シェル要素

要素荷重

圧力荷重および直交収縮による初期歪という、2 つのタイプの要素荷重が利用できます。

圧力荷重は、要素の中間サーフェスに対して、垂直に作用すると仮定します。隣接する要素で使用される圧力値が異なる場合でも、所定の要素全体に一定値の圧力がかかると仮定します。

積分ルール

中間サーフェスに関する積分は、3 点数値求積法を使用して、実行されます。材料は線形弾性で、要素は平坦であるため、歪と応力の両方が、シェルの壁方向に線形に変化します。したがって、負荷のかかる数値積分の代わりに、肉厚方向の陽的事前積分が使用されます。

積分位置の配置と重みを、GUID-C6040A5F-6941-450C-B147-FBC16693CC13.htm#FIG_E1DAFC547406436A9270BF10CBD734FA、および GUID-C6040A5F-6941-450C-B147-FBC16693CC13.htm#TABLE_F179DB3BBB53438FA4CC698971F96BEF に示します。

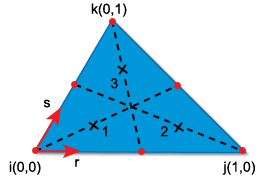
LMT3 要素の積分位置の配置

LMT3 要素の積分位置の重み

要素	積分位置	r-座標	s-座標
LMT3	1 2012 ベータ 2 3	1/6 2/3 1/6	1/6 1/6 2/3

結果出力

膜力 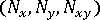、曲げモーメント 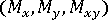、および横せん断力 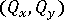をこれらの積分位置で計算して、GUID-C6040A5F-6941-450C-B147-FBC16693CC13.htm#FIG_B99F2DD2E5FD417B8F2AFD4917C09270 に示します。

これらの結果は、解析出力ファイルに複製されます。

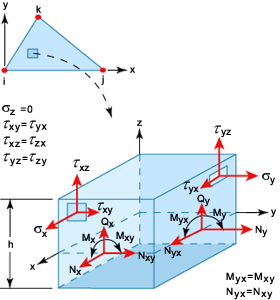
LMT3 要素に関する解析結果

平面応力条件を仮定すると、レベル z における応力は、次の式で計算されます。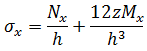

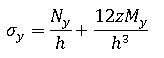
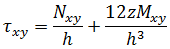
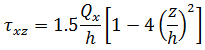力とモーメントは、単位幅のプレートまたはシェルに作用するものです。そのため、膜力とせん断力は「力/長さ」という次元を持ち、モーメントは「力」の次元を持ちます。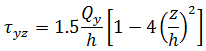

要素 LBT3

Dual Domain 解析では、要素 LMT3 を使用します。LMT3 は、3 つのノードからなる、18 自由度 (各ノードごとに 6 自由度) を持つ三角形要素です。この要素を構成するには、Bergan と Nygard および Bergan と Felippa によるローカルな膜の定式化に、Batoz による曲げの定式化を重ね合わせ、結合した式をグローバル座標系に適合するように変換します。結果として生成される要素は、膜歪、曲げ歪、および横せん断歪の双線形変化をモデル化できます。

Bergan と Nygard の"自由な定式化"は、仮定変位場に基づいていますが、"不適合な"形状関数の使用を許容することにより、ポテンシャル エネルギーの厳密な定式化からは逸脱しています。確実に収束させるために、あらかじめパッチ テストの要件を適用します。変位形状関数は、基本モードと高次モードに分けられます。基本モードは、剛体と一定の歪状態に関連し、高次モードは、座標不変面内曲げモードに関連します。

これが、基本剛性と高次剛性につながり、それぞれ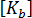 、および 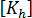で表されます。その結果、合成した膜剛性は、次の形式になります。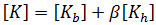

ここで、 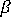は、高次剛性に関する表示倍率となる自由パラメータです。詳細テスト結果に沿って、 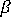= 1.5 が最適な選択として採用されています。

中間サーフェス法線回りの回転(面内回転自由度: ドリリング自由度)で使われる連続体力学定義は、LMT3 に使用されるものと同じです。つまり、次のようになります。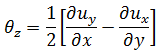

要素の曲げの定式化は一般化されたキルヒホッフの離散的手法に基づいていて、横せん断の影響を考慮しています。この要素は、ロッキングすることなく、厚肉の成形品に対しても薄肉の成形品に対しても解析に有効です。横せん断の影響が大きくない場合には、よく知られた DKT(discrete Kirchhoff triangle: 離散的なキルヒホッフの三角形)要素と一致します。

数値テストによると、この LBT3 は非常に良好な結果を示しています。一般的に、LBT3 の方が、LMT3 よりも若干優れています。さらに、LBT3 ではシングルレイヤーの定式化とマルチレイヤーの定式化の両方が使用できますが、LMT3 は、現時点ではシングルレイヤーの解析にのみ有効です。

繊維充填プラスチックの応力解析および反り解析を実行する際には、マルチレイヤー LBT3 を使用することをお勧めします。繊維配向がレイヤーごとに考慮されるので、物理的モデルがより現実的なものとなり、より正確な結果が期待できます。

要素定義

要素に関する、形状、ノード番号、およびローカル/グローバルな自由度を、GUID-C6040A5F-6941-450C-B147-FBC16693CC13.htm#FIG_AF05FFF4B09B4FBABDC03622AC3CD5FE に示します。ノード i、j、k は、解析出力ファイルに示されているノード接続テーブル内のエントリを指しています。たとえば、要素の接続が 11、101、85 の場合、i = 11、j = 101、k =85 となり、ローカル X 軸の方向は、ノード 11 からノード 101 への方向になります。

LMT3 シェル要素

要素荷重

圧力荷重および直交収縮による初期歪という、2 つのタイプの要素荷重が利用できます。

圧力荷重は、要素の中間サーフェスに対して、垂直に作用すると仮定します。隣接する要素で使用される圧力値が異なる場合でも、所定の要素全体に一定値の圧力がかかると仮定します。

積分ルール

中間サーフェスに関する積分は、3 点数値求積法を使用して、実行されます。材料は線形弾性で、要素は平坦であるため、歪と応力の両方が、シェルの壁方向に線形に変化します。したがって、負荷のかかる数値積分の代わりに、肉厚方向の陽的事前積分が使用されます。

積分位置の配置と重みを、GUID-C6040A5F-6941-450C-B147-FBC16693CC13.htm#FIG_C61B6E2F90EB4797886BED2005A0AAC1、および GUID-C6040A5F-6941-450C-B147-FBC16693CC13.htm#TABLE_8C6B261A81AC44FA8AC435934557AE7C に示します。

LMT3 要素の積分位置の配置

LMT3 要素の積分位置の重み

要素	積分位置	r-座標	s-座標
LBT3	1 2012 ベータ 2 3	1/6 2/3 1/6	1/6 1/6 2/3

結果出力

膜力 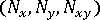、曲げモーメント 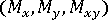、および横せん断力 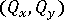をこれらの積分位置で計算して、GUID-C6040A5F-6941-450C-B147-FBC16693CC13.htm#FIG_2BDA74ED49B245BDB26FFD52541E27C1 に示します。

これらの結果は、解析出力ファイルに複製されます。

LMT3 要素に関する解析結果

平面応力条件を仮定すると、レベル z における応力は、次の式で計算されます。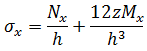

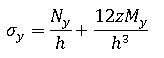
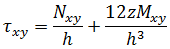
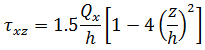
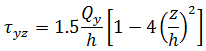
力とモーメントは、単位幅のプレートまたはシェルに作用するものです。そのため、膜力とせん断力は「力/長さ」という次元を持ち、モーメントは「力」の次元を持ちます。

ビーム要素

ビーム要素 BEAM2 は、2 つのノードからなるビームであり、Midplane および DualDomain解析で現在使用可能です。

この要素の長手方向軸は直線であるため、曲面ビームをモデリングする場合は、"ファセット面"の集合体として表示することにより実際の形状に近似させます。現状では、ビームは一定半径の円形断面を持つと仮定されています。ただし、隣接する要素の断面半径は、異なる場合があります。

ノードごとに 6 つの自由度が使用されます。つまり、グローバルな軸に平行な 3 つの移動、およびこれらの軸を回る 3 つの回転です。有限の回転の場合、回転の自由度は、シェルのところで説明した定義とまったく同じです。1 つ以上のノードにおける、ビーム要素とシェル要素の物理的な接続は単純です。すべてのビーム ノードが 1 つのシェル ノードに接続されている場合、結合された構造をモデル化するのに必要な式の合計数は、そのシェル構造を単独でモデル化するのに必要な数と同じです。したがって、ビーム要素を追加する際の計算オーバーヘッドは、一般的に非常に小さくなります。

この要素の定式化により、軸変形、曲げ変形、ねじれ変形、および横せん断変形を処理します。基本的な仮定として、ビーム断面は平面であり歪んでいない、とされますが、横せん断が存在する場合は、長手方向軸に対して垂直でなくなります。その結果、生成されるモデルは、古典的なオイラー - ベルヌーイのビームから 2 つの段階を経て導き出されたものと見なすことができます。まず、Reissner-Mindlin タイプのせん断モデルを追加することにより、横せん断の平均的な影響を計算に含めます。これにより、一般的に、Timoshenko ビームと呼ばれるものになります。次の段階で、St.Venant の理論を利用して、ねじれ挙動をモデル化します。

ビーム要素を用いて、ランナー、リブ、またはスタンドアロン ビーム構造をモデル化する場合、アスペクト比(ビームの軸に沿って測定された全体の長さと、断面の平均直径との比率)は、次の近似範囲内に収める必要があります。

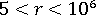
ペナルティ緩和法を使用することで、上限をきわめて高くすることができます。ビーム要素では、シアーロッキングまたはメンブレンロッキングは発生しませんが、この手法により、高いアスペクト比で、要素剛性マトリックスの条件が悪くなることを防ぎます。

現状では、ビーム要素でモデル化できるのは、等方性線形弾性材料のみです。上述した基本的な仮定と矛盾せずに、一般的な直行性材料の挙動を処理することは不可能です。

幾何学的な非線形性は、対流ラグランジュ手法に基づいています。この手法では、変位場が、各点でシェルの断面と共回転する、ローカルな対流座標のセットを参照します。整合性を保つため、ここでは、通常の伸張不可能条件を、任意の点で断面ディレクタと共線性があるファイバーに適用します。

共回転手法は、連続体力学の極分解定理から導き出されます。この定理は、一般的な空間運動は、常に、剛体運動に従う純粋な伸び(変形)に分解できるというものです。適切な有限回転測度を選び、全体的な運動から剛体成分をはっきり切り捨てることで、要素内の内部変形と関連する応力を評価する整合的な方法が実現されます。これは、剛体運動の規模に制限を設ける必要がなく、しかも、内部の変形と応力を決定する際の精度が、解析全体を通して一定のままであるということを意味します。

この定式化の密接に関係するものは、Reissner [11]、Danielson と Hodges [14]、Hodges、および Simo の有限変形理論です。Bates [1] および Simo と Vu-Quoc [15] によるこれらの理論における有限要素の導入も関連があります。

要素 BEAM2

これは、2 つのノードからなる、ノードごとに 6 自由度を持つビームです。ビームの軸は直線であり、断面は円形かつソリッドであると仮定されています。この要素は、スタンドアロン形式で使用することができますが、代わりに、三角形シェル要素 LMT3 の 1 つのエッジに接続することも可能です。

この定式化は、線形アイソパラメトリック形状関数に基づいています。シアーロッキングを避けるために、次数低減積分を使用して、剛性と内力を求めます。この場合、一点ガウス求積法を使用することになります。結果として生成されるモデルは、定まった軸歪、曲げ歪、ねじれ歪、およびせん断歪のフィールドを示します。

変更されない形式では、予測される要素の反応は、その要素が影響を受ける曲げモードに依存します。

純粋な曲げの場合には、制御積分点で、正確なノード変位と合応力が得られます。

しかし、後者の場合の過剰剛性は、ペナルティ緩和法[19]を適用することにより、完全に除去されます。伸びとねじれが一定の場合には、正確な変位と中心の合応力も予測されます。

要素定義:

要素に関する、形状、ノード番号、およびローカル/グローバルな自由度を、GUID-C6040A5F-6941-450C-B147-FBC16693CC13.htm#FIG_9E7E9A1F8F7A41F69AC1D48D5F5ADFB9 に示します。ノード i、j は、解析出力ファイルに示されているノード接続テーブル内のエントリを指しています。たとえば、要素の接続が 55、77 の場合、i = 55、j = 77 となり、ローカル X 軸の方向は、ノード 55 からノード 77 への方向となります。

BEAM2 ビーム要素

要素荷重: 現在使用可能な要素荷重の唯一のタイプは、収縮による軸歪と湾曲歪の指定です。(ただし、外部集中荷重は、力とモーメントであり、有限要素メッシュのノードに直接加えることができます。)

積分ルール

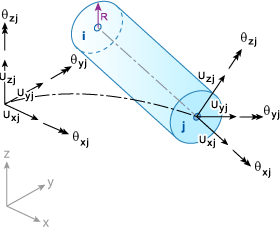
内力(合応力)は、GUID-C6040A5F-6941-450C-B147-FBC16693CC13.htm#FIG_F39597619BAE4B1FA572606A720F781D に示す積分中心点で計算され、解析外部ファイルに複製されます。

線形弾性材料の場合、歪と応力は両方とも、ビーム断面上で線形に変化します。したがって、計算負荷のかかる数値積分の代わりに、断面に関する陽的事前積分が使用されます。

BEAM2 要素の積分位置

.

(a) 積分点

結果出力

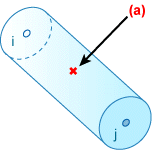
次に示す合応力は、積分位置で計算され、解析出力ファイルに複製されます。

モーメント: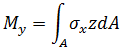

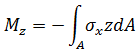ねじれ:

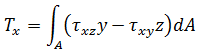力: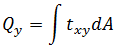

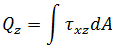
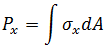
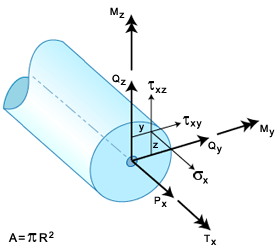
BEAM2 要素に関する解析結果

任意の点(y,z)における応力は、次の式で与えられます。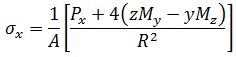

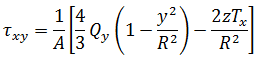
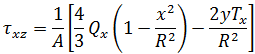
参考資料

1. Argyris, J.H., "An excursion into large rotations", Comp. Meth. Appl. Mech. Engrg., Vol. 32, 1982, pp. 85-155.
2. Rankin, C.C. and Brogan, F.A., "An element independent corotational procedure for the treatment of large rotations", in: Collapse Analysis of Structures (L.H. Sobel and K. Thomas eds.), ASME, New York, 1984, pp. 85-100.
3. Bates, D.N., The mechanics of thin walled structures with special reference to finite rotations, Ph.D. Thesis, University of London, 1987.
4. Hodges, D.H., "Finite rotation and non-linear beam kinematics", Vertica, Vol. 11, No. 1/2, 1987, pp. 297-307.
5. Reissner, E., "The effect of transverse shear deformation on the bending of elastic plates", J. Appl. Mech., ASME, Vol. 12, 1945, A69-A72.
6. Mindlin, R.D., "Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates", J. Appl. Mech., ASME, Vol. 18, 1951, pp. 31-38.
7. Zienkiewicz, O.C., Taylor, R.L., and Too, J.M., "Reduced integration technique in general analysis of plates and shells", Int. J. Num. Meth. Engrg., Vol. 3, 1971, pp. 275-290.
8. Fried, I., "Residual energy balancing technique in the generation of plate bending finite elements", Comp. and Struct., Vol. 4, 1974, pp. 771-778.
9. McNeal, R.H., "A simple quadrilateral shell element", Comp. and Struct., Vol. 8, 1978, pp. 175-183.
10. Tessler, A. and Hughes, T.J.R., "A three-node Mindlin plate element with improved transverse shear", Comp. Meth. Appl. Mech. Engrg., Vol. 50, 1985, pp. 71-101.
11. Reissner, E., "On one-dimensional large-displacement finite-strain beam theory", Stud. Appl. Math., Vol. 52, 1973, pp. 87-95.
12. Reissner, E., "Linear and non-linear theories of shells, in: Thin Shell Structures" (Y.C. Fung and E.E. Sechler, eds.), Prentice-Hall, Englewood Cliffs, New Jersey, 1974, pp.29-44.
13. Simmonds, J.G. and Danielson, D.A., "Non-linear shell theory with finite rotation and stress-function vectors", J. Appl. Mech., ASME, Vol. 39, 1972, pp. 1085-1090.
14. Danielson, D.A. and Hodges, D.H., "Non-linear beam kinematics by decomposition of the rotation tensor", J. Appl. Mech.,ASME, Vol. 54, 1987, pp. 258-262.
15. Simo, J.C. and Vu-Quoc, L., "A three-dimensional finite strain rod model.Part II: Computational aspects", Comp. Meth.Appl. Mech. Engrg., Vol. 58, 1986, pp. 79-116.
16. Bergan, P.G. and Nygård, M.K., "Finite elements with increased freedom in choosing shape functions", Int. J. Num. Meth. Engrg., Vol. 20, 1984, pp. 643-664.
17. Bergan, P.G. and Felippa, C.A., "A triangular membrane element with rotational degrees of freedom", Comp. Meth. Appl. Mech. Engrg., Vol. 50, pp. 25-60.
18. Nygård, M.K., The free formulation for non-linear finite elements with applications to shells, Report No. 86-2, Division of Structural Mechanics, The Norwegian Institute of Technology, Trondheim, 1986.