シェル要素は、3D オリエンテーションにおける 4 から 8 節点のアイソパラメトリック 4 辺形、または 3 から 6 節点の 3 角形要素です。4 節点の要素では、面外の曲げが発生してるモデルの収束変位および応力を提供するために、8 節点の要素に比べ、非常に細やかなメッシュが必要になります。図 1 は、典型的なシェル要素をいくつか示しています。
一般および共回転のシェル要素は、Ahmad、Iron および Zienkiewicz に基づき形成され、その後に Bathe および Balourchi によってリファインされます。厚肉および薄肉シェル両方の問題をモデル化する際に適用できます。また、厚さの変数を含む二重に曲げられたシェルのジオメトリは、このシェル要素を使用して正確に記述することができます。

図 1: サンプルの 3D シェル要素
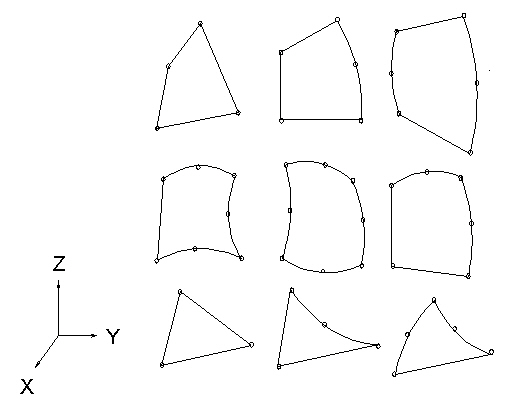
図 2: 典型的なシェル要素
薄肉シェル要素は、薄板理論に基づいています。要素の曲げ動作は、Batoz の補間関数を使用したプレート曲げに対する個別の Kirchoff アプローチに基づいてます。この定式化によって、境界に沿った Kirochoff 拘束が満たされ、要素全体の曲線の線形変動が提供されます。要素の膜動作は、線形ひずみ 3 角形(LST)要素から派生した Allman 3 角形に基づいています。この要素によって、一般的な曲面は、各要素の 3 つの節点によって定義される面によって形成された切り子面のセットとして近似化されます。上記の理由から適切にリファインされたメッシュが必要になります。
要素のジオメトリは、節点ポイントの座標によって記述されます。各シェル要素の節点には、 5 自由度(DOF)が設定されています(3 つの並進および 2 つの回転)。並進 DOF は、全体直交座標系にあります。回転は、各節点に定義されているシェル サーフェス上の2 つの直交軸に基づきます。回転境界条件の制約および適用されたモーメントもこの節点回転系を参照します。2 つの回転軸(V1 および V2)は、通常、プロセッサによって自動的に決定され、その方向を具体的に指定する必要はありません。
各節点の回転 R1 および R2 方向は、次に示すとおり、法線ベクトル Vn と方向ベクトルのクロス積によって決定します。図 3 を参照してください(V1 および V2 はそれぞれ R1 および R2 回転方向に沿った単位ベクトルです)。
R1 = V2 x Vn
R2 = Vn x Vg
既定の方向ベクトル Vg は (1,0,0) です。すなわち、R1 軸は実際にはシェル サーフェス上への方向ベクトル Vg の投影です。R2 軸は、このシェル サーフェス上に存在しますが、R1 および法線ベクトル Vn に対して直交です。図 3 は、既定の方向ベクトル(1,0,0)を使用した R1 および R2 の方向を示しています。
各シェル要素のパーツに対して 2 つの方向ベクトルを入力できます。シェル面に対する方向ベクトルの投影がゼロの場合、2 番目の方向ベクトルが使用されます。特定の節点に対して方向ベクトルを指定することもできます。
プロセッサでは、節点のポイントに接続している異なる要素からの異なる法線ベクトルの平均を使用して、各シェル要素の節点の法線方向が決定されます。要素の法線は、要素の角の節点データから計算されます。この法線ベクトルからは、2 つの回転軸が決定します。法線ベクトルの方向を直接指定して、プロセッサの計算を抑制することもできます。2 つの回転ベクトルは、ユーザ指定の方向に指定することもできます。そのため、3D 空間での傾き回転の制約またはモーメントを容易に定義できます。
複数のシェル パネルが 1 つの領域で交差する場合(通常の場合、交差線)、その領域で回転 DOF を指定することは困難です。この場合、交差領域の節点は 6 自由度の節点として指定します。
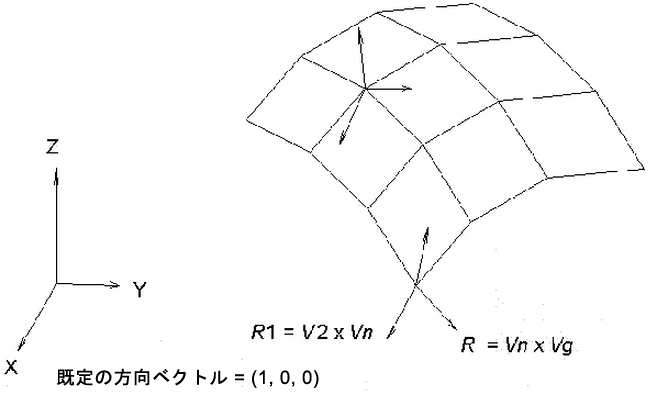
図 3: Vg を使用して決定した回転の自由度[
6 自由度の節点は、各節点に固有の R1 および R2 DOF を持つのではなく、全体に方向設定された回転 DOF を持ちます。
3D のシェル要素は、タイプ 26 要素であり、4 から 8 節点のアイソパラメトリック 4 辺形、または 3 から 6 節点の 3 角形要素です。厚肉および薄肉シェル両方の問題をモデル化する場合に適用できます。また、厚さの変数を含む二重に曲げられたシェルのジオメトリは、このシェル要素を使用して正確に記述することができます。この要素形成の理論的内容は、Bathe および Balourchi で見つけることができます。
要素のジオメトリは、節点ポイントの座標によって記述されます。各シェル要素の節点には、 5 自由度(DOF)が設定されています(3 つの並進および 2 つの回転)。シェル要素の回転 DOF は、シェル方向ベクトルによって定義されます。シェル要素への方向ベクトル Vg の投影は、最初の回転軸(R1)になります。 2 番目の回転軸は、R2 = Vn x Vg という法則の使用により、R1 およびシェル法線ベクトル(Vn)に対して直交です。既定の方向ベクトルは (1,0,0) です。方向ベクトルがシェル法線ベクトル Vn に対して平行である場合、2 番目の方向ベクトル(既定により(0, 1, 0))が R1 の方向の定義に使用されます。
シェル要素パラメータ
シェル要素には、それぞれ異なるオプションを提供する 3 つのタイプが利用可能です。これらのタイプの相違点は、前のセクションで説明されています。シェル要素タイプは、[要素定義]スクリーンの[高度]タブにある[要素定式化]ドロップダウン ボックスで選択できます。ただし、通常の場合、材料モデルに基づいた既定の選択を使用できます。
まず最初に、このパーツの材料モデルを[一般]タブの[材料モデル]ドロップダウン ボックスで指定する必要があります。利用可能なシェル材料モデルは次のとおりです。
- [等方性]: この材料モデル オプションは、応力/ひずみ曲線の弾性領域のみでたわみが生じるパーツに対して使用します。この材料モデルを使用する場合、パーツでは、すべての方向で同一の材料特性が設定されている必要があります。単一のヤング率およびポアソン比が必須の材料特性となります。一般、共回転、薄肉のシェル要素で利用可能です。
- [直交異方性]: この材料モデル オプションは、応力/ひずみ曲線の弾性領域のみでたわみが生じるパーツに対して使用します。パーツでは、一定の方向に異なる材料特性を設定することができます。具体的には、直角座標系の直交方向の 1 つまたは複数の方向で異なる材料特性を設定できます。このオプションは、一般、共回転、薄肉のシェル要素で利用可のです。材料軸の設定に関する詳細については、後述の「シェル要素の方向を制御する」を参照してください。
- [Hardening 等方硬化をともなうフォン ミーゼス]: この材料モデル オプションは、解析中に塑性変形が発生する可能性があるパーツで使用します。双線形曲線を定義して、応力/ひずみの関係を制御します。このオプションは、一般および薄肉シェル要素のみで利用できます。
- [移動硬化によるフォン ミーゼス]: この材料モデル オプションも、解析中に塑性変形が発生する可能性があるパーツで使用します。双線形曲線を定義して、応力/ひずみの関係を制御します。モデルで循環荷重(Bauschinger 効果)が発生する場合は、[Hardening 等方硬化をともなうフォン ミーゼス]材料モデル オプションに対してこの材料モデル オプションの使用を優先します。このオプションは、一般および薄肉シェル要素のみで利用できます。
- [Hardening 等方硬化をともなうフォン ミーゼス曲線]: この材料モデル オプションは、解析中に塑性変形が発生する可能性があるパーツで使用します。複数のデータ ポイントを含む応力/ひずみ曲線を指定して、応力/ひずみの関係を制御できます。このオプションは、一般および薄肉シェル要素のみで利用できます。
- [移動硬化によるフォン ミーゼス曲線]: この材料モデル オプションは、解析中に塑性変形が発生する可能性があるパーツで使用します。複数のデータ ポイントを含む応力/ひずみ曲線を指定して、応力/ひずみの関係を制御できます。モデルで循環荷重(Bauschinger 効果)が発生する場合は、[Hardening 等方硬化をともなうフォン ミーゼス]材料モデル オプションに対してこの材料モデル オプションの使用を優先します。このオプションは、一般および薄肉シェル要素のみで利用できます。
- [Mooney-Rivlin]: この材料モデルは、ゴムなどの超弾性材料のモデル化で使用します。このオプションは、一般シェル要素のみで利用できます。
- [Ogden]: この材料モデルは、ゴムなどの超弾性材料のモデル化で使用します。このオプションは、一般シェル要素のみで利用できます。
- [粘弾性 Ogden]: Ogden (超弾性)材料モデルの粘弾性バリエーションです。このオプションは、一般シェル要素のみで利用できます。
- [粘弾性 Mooney-Rivlin]: Mooney-Rivlin (超弾性)材料モデルの粘弾性バリエーションです。このオプションは、一般シェル要素のみで利用できます。
- [複合材料]: この材料モデルは、複数の層流によって材料特性が影響を受ける複合材料をモデル化する場合に使用します。この材料は、解析中は常に応力/ひずみ曲線の弾性領域に存在している必要があり、その材料特性はすべての温度で同一である必要があります。[複合材料]タブの複合材料の各レイヤに対して材料特性および破損基準を定義する必要があります。このオプションは、共回転シェル要素のみで利用できます。材料軸の設定に関する詳細については、後述の「シェル要素の方向を制御する」を参照してください。
- [温度依存の複合材料]: この材料モデルは、複数の層流によって材料特性が影響を受ける複合材料をモデル化する場合に使用します。この材料は、解析中常に応力/ひずみ曲線の弾性領域に存在している必要があります。その材料特性は温度によって異なります。[複合材料]タブの複合材料の各レイヤに対して材料特性および破壊判定基準を定義する必要があります。このオプションは、共回転シェル要素のみで利用できます。材料軸の設定に関する詳細については、後述の「シェル要素の方向を制御する」を参照してください。
- [熱弾性]: この材料モデルは、応力/ひずみ曲線の弾性領域のみでたわみが発生し、温度差によって応力が発生する可能性がある材料をモデル化する場合に使用します。このオプションは、一般、共回転、薄肉のシェル要素で利用可のです。
- [温度依存の直交異方性]: この材料モデルは、温度変動が発生する一定の方向で異なる材料特性を設定しているパーツで使用します。特に、直交座標系における直交する 3 方向のうち 1 つまたは 2 つの方向の材料特性が異なることがあります。材料特性は複数の温度で指定します。値は、温度値間で線形的に補間されます。材料特性を定義する温度範囲には、目的の温度が含まれていなければなりません。このオプションは、一般、共回転、薄肉のシェル要素で利用可のです。材料軸の設定に関する詳細については、後述の「シェル要素の方向を制御する」を参照してください。
シェル要素の厚さを[厚さ]フィールドで指定します。 要素は、シェル要素の中立面に描画すると考慮されます。解析を実行するには、厚さの値を入力する必要があります。[材料モデル]ドロップダウン ボックスで[複合材料]オプションを選択した場合、このフィールドは利用できません。その場合、このフィールドには[複合材料]タブで定義した層流の厚さの合計が表示されます。
このパーツで、中間節点をアクティブにする必要のあるシェル要素には、[中間節点]ドロップダウン ボックスの[含む]オプションを選択します。このオプションを選択すると、シェル要素では、各エッジの中間点に追加の節点が定義されます。(CAD ソリッド モデルのメッシュの場合、中間節点は、メッシュ作成前に選択したオプションに基づき、CAD サーフェスの元の曲率に従います。手動構築のモデルや変更した CAD モデル メッシュでは、中間節点は、角の節点間の中間点に配置されます。)これにより、4 節点シェル要素が 8 節点シェル要素に変更されます。中間節点を含む要素では、より正確に計算された勾配が結果として生じます。要素に中間節点が含まれる場合、処理時間が長くなります。メッシュが十分に小さい場合は、中間節点を追加しても正確度がそれほど向上しないこともあります。
[解析タイプ]ドロップダウンを使用して、目的とする変位のタイプを設定します。[微小変形]は、モーションが一切なく、小さなひずみのみが発生し、大規模な変形による非線形の幾何学的効果を無視するパーツに適しています。[大変形]は、モーションおよび/または大規模なひずみが発生するパーツに適しています。(選択したシェル要素のタイプによって異なりますが、[高度]タブの[解析定式化]のそのほかのオプションは、[解析タイプ]ドロップダウンの影響を受ける場合があります。)
- 中間節点の変位は常に出力されます。中間節点の応力とひずみは、ユーザが解析前にこれらの結果の出力をアクティブにした場合のみ出力されます。このオプションは、[出力]タブの[設定]
 [モデル設定]
[モデル設定]  [パラメータ]
[パラメータ]  [高度]ダイアログにあります。(詳細については、「解析の設定と実行」の「非線形」の「解析パラメータ」の「高度な設定」の「出力ファイルを制御する」を参照してください)
[高度]ダイアログにあります。(詳細については、「解析の設定と実行」の「非線形」の「解析パラメータ」の「高度な設定」の「出力ファイルを制御する」を参照してください) 
 [オプション]
[オプション] [解析]タブを使用して、[非線形解析のための既定として大変形を使用]オプションを使用して、[解析タイプ]の既定を小変形または大変形に設定します。
[解析]タブを使用して、[非線形解析のための既定として大変形を使用]オプションを使用して、[解析タイプ]の既定を小変形または大変形に設定します。
複合材料モデル
シェル要素で複合材料モデルを使用する場合、[要素定義]ダイアログの[複合材料]タブにある[破壊判定基準]ドロップダウン ボックスを使用して、破壊判定基準を選択できます。利用可能なオプションおよび対応する数式は次のとおりです。
- [Tsai-Wu]: このオプションを選択すると、パーツが構造解析に失敗したかどうかを判別するために Tsai-Wu (または二次テンソル多項式)基準が使用されます。2 方向における応力間の相互作用を考慮する、平面応力条件下にある直交異方性のレイヤに対するこの基準は、次の数式によって決定します。
|
|
(1) |
ここで
![]()
![]()
![]()
![]()
![]()
X t = 引張状態における軸強度または縦強度(>0)
X c = 圧縮状態における軸強度または縦強度(>0)
Y t = 引張状態における横強度(>0)
Y c = 圧縮状態における横強度(>0)
S = せん断強度
F12 = 材料特性に入力した応力相互作用の値。値が 0 の場合、既定の ![]() が使用されます。
が使用されます。
σ 1 = 主材料 1- 方向の応力
σ 2 = 主材料 2- 方向の応力
τ 1 2 = 主材料 1-2 面のせん断応力
数式が (1) が満たされない場合、材料が失敗したことを示します。
![]() (2)
(2)
R は、強さ/応力の比率です。
(1) における応力コンポーネントの各組み合せは左側が単一になるとその最高値となるため、(2) を (1) に代入して次の解を得ることができます。
![]()
R を得るための計算式の解法:
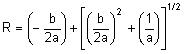
ここで
![]()
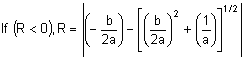
応力を示す記号 σ ij は反転しています。
- [応力の最大値]: このオプションを選択すると、 パーツが構造解析に失敗したかどうかを判別するために最大応力基準を使用します。提供されている基準は次のとおりです。
|
|
内容
σ 1 = 1 つの方向における計算済み応力
σ 2 = 2 方向の算出済み応力
τ 1 2 = 算出済みのせん断応力
X c = 1 方向の許容圧縮応力(>0)
Yc = 2 つの方向における許容可能な圧縮応力(>0)
X t = 1 方向の許容引張応力(>0)
Y t = 2 方向の許容引張応力(>0)
S = 許容せん断応力(>0)
数式 (3) の 3 つの条件が満たされない場合、材料が失敗していたことを示します。
- [ひずみの最大値]: このオプションを選択すると、 パーツが構造解析に失敗したかどうかを判別するために最大ひずみ基準を使用します。提供されている基準は次のとおりです。
|
|
内容
ε 1 = 1 方向の算出済みひずみ
ε 2 = 2 方向の算出済みひずみ
γ = 算出済みせん断ひずみ
T 1c = 1 方向の許容圧縮ひずみ(>0)
T 2c = 2 つの方向における許容可能な圧縮ひずみ(>0)
T 1t = 1 方向の許容引張ひずみ(>0)
T 2t = 2 方向の許容引張ひずみ(>0)
S = 許容可能なせん断ひずみ(>0)
計算式 (4) の各条件が満たされない場合、その材料はエラーとなります。
[複合材の積レイヤシークエンス]表は、複合材料のレイヤを定義するのに使用できます。レイヤには、後述の「シェル要素の方向を制御する」で説明する方向および順序が設定されます。各レイヤには、[厚さ]列を定義する必要があります。[方向角]列は、材料座標軸( Orientationタブで定義)と繊維座標軸またはレイヤ座標軸との角度αを提供します。材料特性は、レイヤ座標軸に基づき入力します。レイヤの材料特性を定義するには、[材料]列内をクリックします。 既存の材料を選択するか、新しい材料を[追加]できるダイアログが表示されます。(詳細については、「解析の設定と実行」の「非線形」の「材料特性」の「複合材料特性」を参照してください)
シェル要素の熱特性の定義
シェル要素のパーツで熱弾性または温度依存の材料モデルを使用している場合、[要素定義]ダイアログの[熱]タブにある[応力なしの参照温度]フィールドに値を指定する必要があります。この値は、節点温度の双線形補間を使用して、熱増加の拘束に関連する要素ベースの荷重を算出するための参照温度として使用されます。
シェル要素の方向を制御する
ユーザが制御できる軸には 2 つのタイプがあります。 そのひとつは、シェル要素に対して法線の軸です。法線方向を指定する主な理由は、要素に対する圧力の適用またはサーフェス間接触の指定を実行するためです。複合材料の場合、垂直方向によって、要素レイヤ 1 のどの辺が上になるかが制御されます。2 つ目は要素の面内軸です。これは、直交性材料モデルを使用する場合、または要素の座標系で結果を取得する場合に役立ちます。
これら 2 つのタイプに加え、ユーザが以下の設定を行う必要のある三軸系もあります。
- 要素軸。
- 材料軸。直交性材料および複合材料モデルに使用されます。
- 積層軸。複合材料モデルとともに使用されます。
[要素軸]:
要素標準ポイントは、要素の法線軸 (+3) の方向を制御したり、または要素の側面が上側(+3 側)および下側(-3 側)であるかを制御するために使用します。法線方向は、[方向]タブの[要素法線]セクションの[X 座標]、[Y 座標]および[Z 座標]フィールドを使用して空間内のポイントを定義することで決定します。図 4 を参照してください。 正の垂直方向の圧力は、+3 軸の方向でシェル要素に対して垂直に適用されるため、要素標準点から離れた方向に向きます。
|
| 図 3: 要素法線の決定 シェル要素のエッジを基点にしたビューを示しています。 |
一般的な FEA 解析では、要素の面内方向である軸 1 および 2 を無視できます。要素の面内軸の方向設定は、直交性材料モデルの要素や複合材料要素で便利です。軸 1 および 2 の方向は、[要素定義]ダイアログの[方向]タブで設定します。
[方法]ドロップダウン ボックスには、要素のどちら側面が ij 側になるのかを指定する場合に使用できる 3 つのオプションがあります。要素軸 1 は、要素の ij 側に対して平行です。(要素軸 2 は、軸 1 および 3 で右手系を形成します。)
- [既定]オプションを選択すると、最も高いサーフェス番号を持つ要素の側面が ij 側として選択されます。
- [I 節点方位]オプションを選択すると、[X 座標]、[Y 座標]および[Z 座標]フィールドで座標を定義する必要があります。この点に最も近い要素の節点が、i 節点として指定されます。j 節点は、要素の法線軸(+3 軸)に対する右手の法則に従い、要素のその次の節点になります。
- [IJ 節点方位]オプションを選択した場合、[節点オーダ]セクションの[X 座標]、[Y 座標]および[Z 座標]フィールドで座標を定義する必要があります。この点に最も近い要素の側面が、ij 側として指定されます。i および j 節点が割り当てられ、i 節点から要素に沿って、要素の垂直軸に関する右手の法則(+3 軸)に従うことによって j 節点に到達可能となります。
材料軸:
材料特性は、直交性モデルの材料軸について入力します。材料軸は、[要素定義]ダイアログの[方向]タブにある[材料軸方向指定]セクションを使用して、要素軸(または全体参照)から定義できます。(複合材料の材料特性は、後述のとおり、レイヤ軸について入力します。)
すべての場合において、材料軸 3 は、要素に対して垂直で、要素軸 3 と同じ方向になります。
拡張シェル要素で直交性または複合材料のモデルを使用している場合、面内材料軸 1 および 2 は次のように定義できます。
- [方法]ドロップダウン ボックスで[要素]オプションを選択すると、材料軸は要素ローカル軸に基づきます。[内面の回転角]で変更を加えていない限り、材料 1 および 2 軸は、要素 1 および 2 軸に対して平行です。
- [全体 X-軸]オプションを選択すると、要素に対する全体 X 軸の投影によって軸 1 が作成されます。
- [全体 Y-軸]オプションを選択すると、要素に対する全体 Y 軸の投影によって軸 1 が作成されます。
- [全体 Z-軸]オプションを選択すると、要素に対する全体 Z 軸の投影によって軸 1 が作成されます。
- [ポイント]オプションを選択すると、[X 座標]、[Y 座標]および[Z 座標]フィールドでポイントが定義されます。材料軸 1 は、ユーザ定義のポイントから各統合ポイントまたはガウス ポイントへの方向になります(さらに、要素の面に投影されます)。基本的に、これによって軸 1 がラジアル方向に配置されます。材料軸 2 は、要素の面にあり、軸 1 および 3 と共に右手系を形成します。
- [ベクトル]オプションを選択した場合、[X 座標]、[Y 座標]および[Z 座標]フィールドでベクトルを定義します。材料軸 1 は、定義したベクトルに対して平行です。材料軸 2 は、要素の面にあり、軸 1 および 3 と共に右手系を形成します。
共回転シェル要素の材料軸の方向設定に使用した方法に関わらず、[面内の回転角]フィールドを使用して、指定した角度単位で材料軸を軸 3 の周りで回転させることができます。回転は、軸 3 に対する右手の法則に従います。
一般シェル要素で直交性材料モデルを使用している場合、面内材料軸 1 および 2 は次の 2 つの方法を使用して方向設定することができます。最初の方法では、[X 方向]、[Y 方向]、[Z 方向]フィールドを使用して、材料軸 1 に平行なベクトルを定義します。材料軸 2 は、要素の面にあり、軸 1 および 3 と共に右手系を形成します。2 番目の方法では、[材料軸回転角]フィールドで角度を定義します。この角度により、材料軸 1 は、右手の法則に基づき要素 3 軸の周りを回転します。この方法は、[X 方向]、[Y 方向]、[Z 方向]フィールドの値が 0 の場合のみ使用できます。
図 5: 材料軸の方向の回転角度の定義
レイヤ軸:
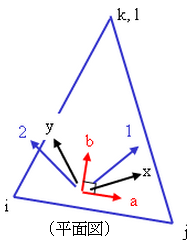
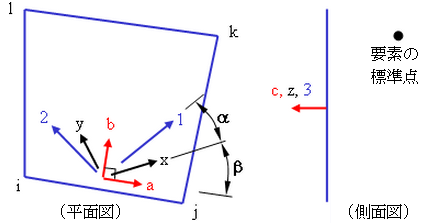
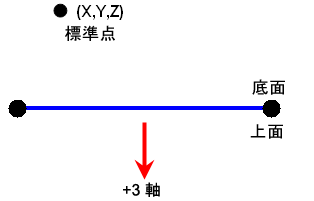
複合材料の場合、積レイヤの各レイヤには、一組のローカル軸があります。レイヤ 1 軸は、個別のレイヤのファイバーに沿った軸です。レイヤ 2 軸は、個別のレイヤのファイバーに対して垂直、かつ要素の平面にある軸です。レイヤ 3-軸は、要素に対して垂直であり、したがってローカル要素軸 c に対して平行です(レイヤ軸と要素軸との混乱を避けるため、複合材料での作業では要素軸はしばしば a-b-c で参照され、繊維の方向は軸 1-2-3 で定義されます)。 図 6 および 7 を参照してください。
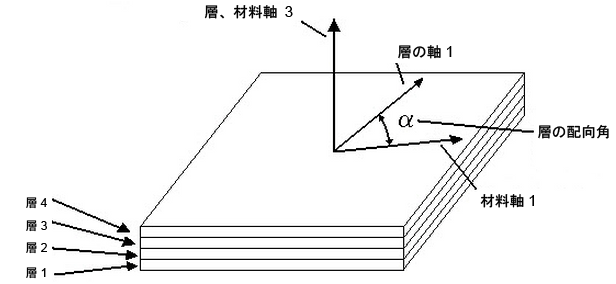
図 6: 積層オーダ
[複合材の積レイヤシークエンス]表の[方向角]を使用して、各レイヤの角度を入力します。軸 3 は、要素基準座標によって制御されます。
|
|
|
図 7: 要素軸、材料軸、レイヤ軸の代替描画
要素軸 a-b-c は、要素基準座標および要素の ij 側に基づいています。材料軸 x-y-z は、要素軸から角度 b 回転します。要素軸および材料軸は、積レイヤのすべてのレイヤで同じです。レイヤ軸または繊維軸 1-2-3 は、材料軸から β 回転します。さらに、積レイヤの各レイヤでは、異なる角度を回転できます。 |
高度なシェル要素パラメータ
[高度]タブの[解析定式化]ドロップダウン ボックスを使用して、シェル要素に使用する定式化方法を選択します。
- [非線形材料に限る]オプションを選択すると(一般シェル要素)、非線形材料モデルの効果は考慮されますが、すべての計算は変形していないジオメトリに基づき実行されます。したがって、この定式化は、モーションのない、小さなひずみがあるパーツに適しています。
- [Total Lagrangian 法]オプション(一般および薄肉シェル要素)では、すべての静的および運動学的変数に対して、変形されていない初期構成が参照されます。この定式化は、モーションおよび小さなひずみがあるパーツに適しています。材料特性は、エンジニア上の応力とひずみについてであることに注意してください。
- [Updated Lagrangian 法]オプション(一般シェル要素)では、すべての静的および運動学的変数に対して、モデルの最後に計算された設定が参照されます。この定式化は、モーションおよび大きなひずみがあるパーツに適しています。材料特性は、実際の応力とひずみについてであることに注意してください。
- [線形]オプション(一般および薄肉シェル要素)では、大きな変形の結果生じた非線形の幾何学的効果が無視されます。
- [幾何非線形]オプション(共回転シェル要素)では、大きな変形の結果生じた非線形の幾何学的効果が含まれます。
[要素の重なりを許可]チェック ボックスをアクティブにすると、線形を要素に変換する場合に重なる要素の作成が許可されます。要素をモデル化する際に重なりが必要となることがあります。これは特に、平面モーションに限られた問題で当てはまります。
解析中に各時間ステップごとに各要素の応力結果をテキスト ログ ファイルに書き込むには、[詳細な応力出力]チェック ボックスをアクティブにします。その場合、出力の量が大きくなる場合があります。
フォン ミーゼス材料モデルのいずれかを選択した場合、現在の材料の状態(弾性または塑性)、現在の降伏応力制限、現在の等価応力制限および角の節点の等価塑性ひずみ出力、および/または各時間ステップの統合ポイントを含むよう選択できます。これは、[追加の出力]ドロップダウン メニューで適切なオプションを選択して行います。
一般シェル要素を使用している場合、パーツで使用する積分オーダを[積分オーダ]ドロップダウン ボックスで選択します。長方形の要素には、[第 2 オーダ]を選択します。中程度に変形した要素の場合は、[第 3 オーダ]を選択します。過度に変形した要素には、[第 4 オーダ]を選択します。要素剛性の定式化にかかる計算時間は、積分オーダの 3 乗に比例して増大します。したがって、受け入れ可能な結果を生成する最も低い積分オーダを使用すると、処理時間を短縮できます。
低減積分スキーマは、[膜せん断項の低減積分]または[横せん断項の低減積分]チェック ボックスをアクティブにすることによって、曲線シェル設定のせん断ロック動作を向上させるために使用できます。シェル要素の厚さがその長さまたは高さの 1/10 未満の場合、低減積分をお勧めします。シェル要素の厚さがその長さまたは高さの 1/10 より大きいの場合、完全な積分をお勧めします。
シェル要素が厚肉か薄肉かを特定する方法
個別の要素の特性長について、シェル要素の細長さが考慮されます。細長さは、特性長で除算した厚さとして定義されます。特性長と厚さを特定するには、次の手順を実行します。
- [ツール] > [計測]を選択して頂点を 2 つクリックし、頂点間の距離を取得します。
- [要素定義]ダイアログ ボックスの[一般]タブで、シェル要素の厚さを定義します。
- [ツール] > [最小/最大の長さ]を選択して、モデルを構成する線の最小と最大の長さを指定します。これはグローバルなツールであるため、長さの照会で考慮しないパーツは非表示にします。
注: 一般シェルの要素式は厚肉シェルと薄肉シェルの両方に適用することができます。また、適切な解析定式化または[膜せん断項の低減積分]オプションを使用して、モデルをリファインすることもできます。これらの設定は、[要素定義]ダイアログ ボックスの[高度]タブで行います。要素式およびオプションを選択する際は、次の点を考慮してください。
-
細長さ > 1/10:
横せん断剛性が重要である場合(つまり、横せん断を考慮することが結果に大きな影響を及ぼす場合)、常に厚肉シェルが必要となります。均質な等方性シェル要素の場合、細長さが約 1/10 を超えると、横せん断剛性が重要となります。したがって、このような場合は一般シェルを使用し、[膜せん断項の低減積分]オプションは有効にしないでください。
-
細長さ < = 1/10:
横せん断剛性が副次的または重要でない場合、および Kirchhoff 拘束(下記を参照)を正確に満たす必要がある場合、薄肉シェルが必要となります。これは、シェルが均質で細長さが約 1/10 未満である場合に該当します。したがって、このような場合は、[薄肉]シェルを指定するか、[一般]シェルを使用できますが、[膜せん断項の低減積分]オプションをアクティブにします。
- [膜せん断項の低減積分]オプションは、[一般]シェル要素を使用した、すべての非線形解析に適用できます(MES 解析、非線形材料による静解析、非線形材料による固有値解析、Riks 解析)。
- 一般シェルでは、せん断ロックが発生する場合があります。薄肉要素に一般シェルを使用しており、せん断ロックが発生する場合は、[膜せん断項の低減積分]オプションを有効にする必要が生じることがあります。せん断ロックは、大幅に低く見積もったせん断変位として特徴付けられます。非線形モード解析の場合、この現象によって過剰に高い固有値が計算されることがあります。
- 通常、せん断ロックが発生すると、高周波振動やその他の構造物の不安定性など、重要なパラメータに関係なく、粗いメッシュの収束率が低下します。細長さがなお 1/10 以下である場合、[膜せん断項の低減積分]オプションを使用する前に、メッシュの品質や過度な粗さに関する問題をまず解決することをお勧めします。
Kirchhoff 拘束:
薄肉シェル理論では、要素法線はシェルの基準サーフェスに対して直交した状態が維持されます。これを Kirchhoff 拘束と呼びます。これをグラフィカルに示したのが次の図です。赤い線は要素法線を表し、マゼンタの線は中立面(基準サーフェス)のエッジです。
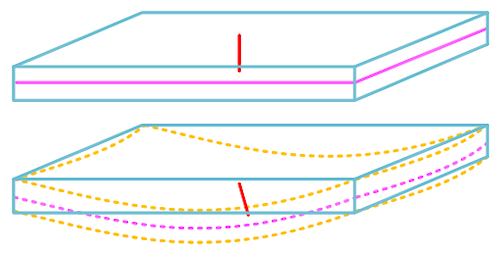
共回転シェル要素
一般および薄肉に加え、共回転シェルの要素式も使用できます。この定式化では、複合材料および熱材料について安定性の高い解析を行うことができます。従来、共回転シェル要素は「拡張」シェルと呼ばれていました。
共回転シェル要素では、[ドリル自由度を抑制]チェック ボックスをアクティブにして、モデルの収束を支援することができます。このオプションは、モデルでローカル座標系を使用している場合使用できません。
シェル要素の使用の基本手順
- 単位系が定義されていることを確認します。
- モデルで非線形解析タイプを使用していることを確認します。
- シェル要素に設定するパーツの[要素タイプ]の見出しを右クリックします。
- [シェル]コマンドを選択します。
- [要素定義]の見出しを右クリックします。
- [要素定義を編集]コマンドを選択します。
- [一般]タブで、[材料モデル]ドロップダウン ボックスから適切な材料モデルを選択します。
- シェル要素の[厚さ]を入力します。これは必須情報で、その入力なしではモデルは実行されません。
- [材料モデル]ドロップダウン ボックスで[複合材料]または[温度依存の複合材料]オプションを選択した場合は、[複合材料]タブで適切なデータを指定します。
- [方向]タブをクリックします。
- 要素標準ポイントを指定します。シェル要素のトップ部分は、常にこのポイントから離れた方向を向きます。
- [OK]ボタンを押します。
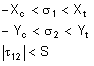 (3)
(3) 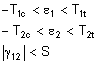 (4)
(4)