プロセスの概要
熱伝導率が温度の関数である場合(直交異方性材料モデル)、またはモデルに輻射が適用される場合、反復を複数回実行して定常熱伝導解析問題を解く必要があります。たとえば、温度が不明だと熱伝導率はわかりませんが、熱伝導率がわからなければ温度を計算できません。したがって、反復という手法が必要となります。
温度に依存する熱伝導率および輻射は解析の単純化を目的として使用されるだけでなく、物体間輻射および熱伝達を温度の関数として計算する際にも利用されます。詳細はこの後のセクションを参照してください。
定常ソルバーの各反復では、温度に依存する熱伝導率および輻射熱伝達率は節点温度の事前推定値(T i cur)に基づいて予測されます。最初の反復では、節点に個別に適用される値(節点を右クリックして[追加] > [温度]コマンドを選択)またはグローバルに適用される値([解析パラメーター]画面の[オプション]タブにある[節点温度の既定値])のいずれかによって初期温度が与えられます。節点の初期温度の値が FEA エディタ環境で指定されると、既定値に対しこれらの値が優先されます。この状態でモデルの解析が実行されます。計算結果として得られた温度(Ti new )が節点温度の事前推定値と比較されます。下記のとおり、事前の推定温度と結果の温度の差が許容できる場合は、解析の反復が終了します。この差が許容できない場合は、新たな節点温度の推定値に基づき熱伝導率と輻射熱伝達率が再計算され、再度解析が実行されます。このプロセスを示したのが図 1 です。
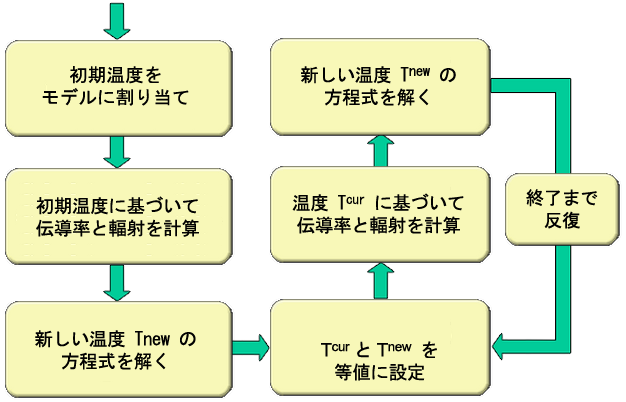
図 1: 非線形解析プロセス
実際には、次の反復での熱伝導率または輻射の計算に使用される温度(T cur )は、[(1-A)(T i old )+(A)(T i new )]、または同等の式[T i old +A(T i new -T i old )]として計算されます。ここで、A は緩和パラメータ([解析パラメーター]画面の[高度]タブにある[緩和パラメータ]フィールドで指定)、T i old は前回の反復で計算された温度です。値 A は、通常は 1 にすることが推奨されます。次の反復で使用される推定温度は、今回の反復計算から得られた温度(T i new )です。オーバーシュートが発生する可能性を排除するために温度T cur をわずかに更新する必要がある場合は、0 と 1 の間の値が使用されます。緩和パラメータの値を 0 (ゼロ)にすると温度が更新されなくなるため、ゼロ以外の値を使用してください。緩和パラメータを 1 以外の値にする必要があるのは、連続的な反復の間に節点温度が循環し、滑らかに収束しない場合です。
新しい推定温度を用いて熱伝導率が更新され輻射方程式が再計算されて、プロセスが繰り返されます。
温度の関数としての熱伝導
直交異方性材料モデルを使用する場合は、熱伝導率を温度の関数として指定することができます。伝導率の値に対応する温度の値を指定します。直交異方性特性は、温度の昇順で指定する必要があります。解に見られる温度の範囲は、材料特性が指定された温度の上限または下限を超えてはいけません。熱伝導率は、指定された温度値間を線形補間することにより計算されます。
初期温度の既定値は 0 (ゼロ)です。温度変化がない場合、熱伝導率を決めるために指定する最小温度は 0 以下にします。初期温度は、熱伝導率の初期値を求めるために使用されます。熱伝導率を更新するために、温度に対して前述の非線形オプションを用いて反復します。
輻射
輻射を受けるサーフェスに発生する熱流束(単位時間、単位面積当たりの熱伝達)は、次の式で表されます。
ただし、
- q = 熱流束
- F rad = 輻射率(吸収率、放射率、および視覚係数の影響を含む)
- σ = Stefan-Boltzmann 定数
- X = [解析パラメーター]画面で入力する輻射乗数
- T s = 計算により求められたサーフェス温度(単位は絶対温度、すなわちランキンまたはケルビン)
- T rad = 環境温度(単位は絶対温度、すなわちランキンまたはケルビン)
サーフェスベースの荷重であることから、輻射のパラメータ F rad および Trad は、[サーフェス特性]画面の[輻射]タブで指定します。モデルの温度は華氏またはセ氏で入力できます。この温度は、[解析パラメーター]画面の[輻射]タブで入力することにより、絶対温度に変換されます。この画面で、Stefan-Boltzmann 定数も指定します。
量(T s 4 -T rad 4 )は、(T s 2 +T rad 2 )(T s +T rad )(T s -T rad )と書き換えることができます。(T s 2 +T rad 2 )(T s +T rad )を定数とみなす場合は、線形解法のアルゴリズムを使用できます。非線形実行時オプションでは、T i old を式の定数部分の Ts に代用し、前述したように反復を実行します。反復の過程で解が振動する場合は、緩和パラメータ(A)を適宜小さくすることが必要です。
物体間輻射
前述した輻射のタイプは、周辺環境に輻射するパーツに当てはまります。実際には、輻射による熱伝達には同じパーツの他のサーフェスや他のパーツが関与していることがほとんどです。表示領域内で右クリックし、[物体間輻射]コマンドを選択するか、[設定] 
[熱荷重] [物体間輻射]を選択します。輻射によって互いに熱を伝達し合う各サーフェスは、それぞれ別個のエンクロージャ内に配置することができます。これらのサーフェスの放射率を、定数値または温度に依存する値として定義できます。詳細については、「物体間輻射」を参照してください。
場合によっては、物体間輻射は、次の図に示すように温度依存熱伝導率を用いて再現することが可能です。
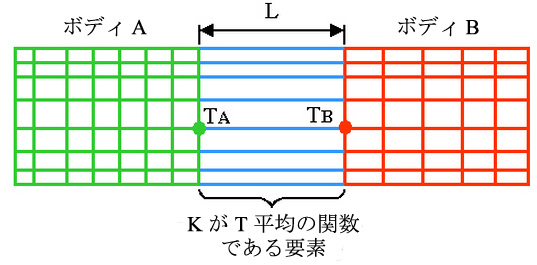
図 2: 物体間輻射
この近似を正確にするための条件は次のとおりです。
- 物体間の形態係数を 1 に近付ける。
- システムからの熱流束は無視できる、つまり、周辺環境への輻射はないものとする。
- 各物体のサーフェス積が等しい。
- サーフェスの推定温度は、手計算、実験、前の解析(複数反復による)のいずれかからわかっている。
向かい合う 2 つの物体間で熱交換が行われ、物体のサーフェス抵抗および空隙抵抗は考慮されないものとします。このとき、次の式が成り立ちます。
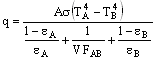
ただし、T A および T B はサーフェス A および B の温度(単位は絶対温度)、ε A および ε B はサーフェス A および B の放射率、VF AB は 2 つのサーフェスの間の形態係数です。
2 つの物体間の熱伝導による熱流束は次の式で表されます。
輻射による熱流束は熱伝導による熱流束と等しいので、上の 2 つの式と、
の展開式
から次の等式が得られます。
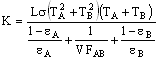
ただし、温度は絶対温度とします。
2 つの物体間の新しい部分に、要素のレイヤが 1 つ作成されます。材料特性が温度依存性を持つようにするため、材料モデルを直交異方性に設定します。熱伝導率は、上の式を使って、推定サーフェス温度 T A および T B (単位は絶対温度)で計算します。熱伝導率の計算値が、温度 Taverage=0.5(T A +T B ) (単位は絶対温度または[単位定義]ダイアログで設定した温度単位)で材料特性に入力されます。別の値の T A および T B で T average および K を求めることにより、追加のデータ ポイントが入力されます。温度の計算値が材料特性の範囲に収まるようにするため、材料特性には必ず温度 T average の範囲を指定するようにしてください。
- 物体間輻射の近似では、範囲 L の要素を 1 つだけ使用します。方向 L のメッシュは使用しないでください。
- T A と T B の値の組み合わせが変わると、熱伝導率 K は変化します。T average が一定の場合、与えられた T average に対して得られる熱伝導率全体の平均値が K として入力されます。
温度の関数としての熱荷重
定常熱伝導解析の実行中、熱伝達荷重や発熱荷重は温度変化に応じて変わることがあります。温度に依存する熱伝達荷重を適用するには、[サーフェス特性]画面に移動し、[熱伝達]タブの[温度依存の熱伝達係数]チェックボックスをオンにします。次に、サーフェスでの熱伝達による熱流量を調べるための熱伝達係数対温度曲線を定義します。温度に依存する発熱荷重を適用するには、[要素定義]に移動し、[荷重]タブの[温度に依存]チェックボックスをオンにします。その後に、このパーツでの発熱を調べるための発熱率対温度曲線を定義します。