Выбор кривой

При использовании устройства графического ввода для задания значений, которые изменяются в процессе моделирования , можно выбрать один из нескольких вариантов описания секторов кривой . Речь идет об определенных формулах или математических функциях, с помощью которых создаются конкретные типы кривой.

Прим.: Если значения расчетных параметров используются в формулах, определяемых пользователем, к именам этих параметров в браузере добавляются в скобках имена параметров, для расчета которых используются полученные значения. Например: "Сила (Вращение:7)"

Выбор математических функций и задание их параметров

Для описания секторов кривой необходимо задать для них математические функции (формулы). Можно создать несколько последовательных секторов, для каждого из которых будет задана определенная формула или группа формул, например функция синуса и линейно нарастающая функция. Можно, например, создать первый сектор с использованием кубической зависимости, а второй - с использованием функции синуса. В программе для глобальных формул действует принцип непрерывности. По этой причине первая точка второго сектора может совпасть с последней точкой первого сектора, в результате чего остальные точки будут автоматически смещены. Часто для получения нужной кривой необходимо добавить дополнительные функции.

После выбора формулы и перемещения ее в "Список формул сектора" необходимо задать ее параметры. Чтобы добавить параметры, необходимо выполнить следующие действия.

После выбора сектора кривой и добавления условий, которые требуется применить, можно задать для сектора параметры.

В поле "Список формул" щелкните стрелку вниз и выберите нужную формулу.
Щелкните стрелку , чтобы заменить текущую формулу сектора на формулу, выбранную в списке.
По мере необходимости формулы можно постоянно менять, при этом новая формула будет заменять формулу из списка.

Для одного вектора можно использовать несколько формул. Если необходимо добавить для сектора дополнительные формулы, выполните повторно шаги первый и второй и нажмите кнопку . Для удаления одной из формул, заданных для сектора, выберите в списке формулу, которую требуется удалить, и нажмите кнопку .

Введите необходимые свойства для формулы, которая отображается в поле "Список формул".

При отображении

Введите свойства

Линейное, Кубическое, Центр масс, Гармонический, Модифицированная синусоида, Модифицированный трапезоид

координаты (X1, Y1) и (X2, Y2) точек, определяющих кривую, и/или введите значение для параметра Уклон, чтобы задать средний градиент отрезка. Кривую можно определить путем ввода координат начальной и конечной точек или координат начальной точки и среднего градиента сектора.

Кривая зеркально отраженна относительно середины сектора.

Область под кривой равна площади треугольника, который образуется под эквивалентным линейным наклоном.

Линейный наклон - это постоянный уклон, который образуется при соединении двух точек прямой линией.

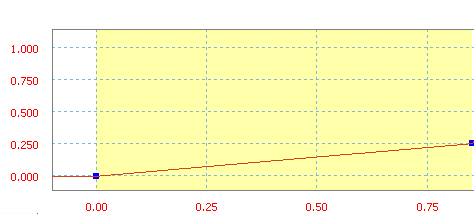
Линейная характеристика с уклоном 30 дюймов/с.

Кубическая функция описывается с помощью полинома 3-й степени.

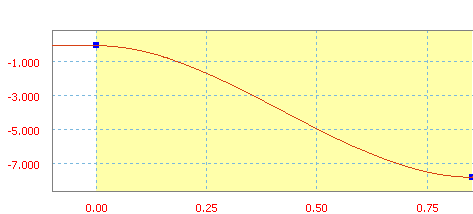
Кубическая характеристика со средним уклоном 70 дюймов/с.

Циклоида - это линейно нарастающая функция синуса/косинуса.

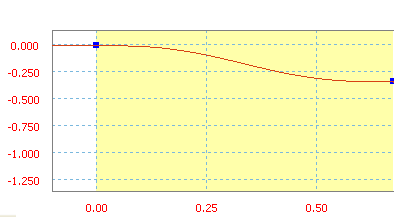
Средним уклон циклоиды -50 дюймов/с.

Гармоническая формула - это линейно нарастающая функция синуса/косинуса.

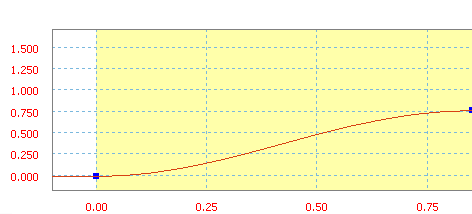
Гармоническая характеристика со средним уклоном 90 дюймов/с.

Преобразованный синус - это линейно нарастающая функция синуса/косинуса.

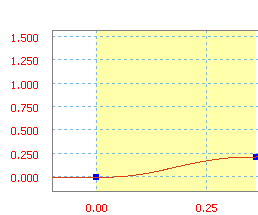
Преобразованный синус со средним уклоном 60 дюймов/с.

Модифицированный трапезоид - это линейно нарастающая функция синуса/косинуса.

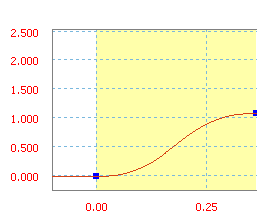
Модифицированный трапезоид со средним уклоном 300 дюймов/с.

При отображении	введите
Синусоидальная	значение для параметра Амплитуда, чтобы задать высоту кривой от медианы цикла, значение для параметра Частота, чтобы задать число циклов за единицу по оси X, и значение для параметра Фаза, чтобы задать расстояние от начала цикла до начала сектора. Синус - это классическая функция. Единицы измерения амплитуды идентичны единицам измерения управляемой переменной (вынужденное движение, сила). Единицы измерения частоты - обратные единицы переменной, используемой для оси X (Гц, если речь идет о времени). Фаза измеряется в градусах или радианах.
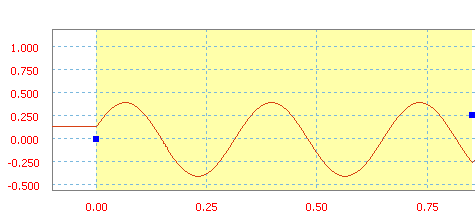
Синус с амплитудой 40, частотой - 3 Гц и фазой - 20 градусов.
Полиномиальная	Полином - это степенная функция, в данном случае она имеет до 5 степеней. Существует два метода определения коэффициентов для полинома. Метод 1 - указание значений коэффициентов Введите значение для a0, а также для всех остальных необходимых параметров a. Метод 2 - импорт текстового файла С помощью отображается диалоговое окно открытия, которое позволяет импортировать файл, определяющий этот полином. С помощью параметра Порядок задается порядок полиномов для кривой в выбранном секторе. С помощью кнопки выполняется расчет значения констант и значений при первых пяти элементах степенного ряда этого полинома. a0, a1, a2, a3, a4, a5 - отображение значений констант и значений при первых пяти элементах степенного ряда этого полинома. При необходимости эти значения можно изменить. Текстовый файл должен быть отформатирован следующим образом: //примечания - примечания не являются обязательными, в начале добавляются две косые черты. x1 y1 - список точек с использованием значений x и y. ... - определение одной точки в ряду или строке. xn yn - определение нужного количества точек. Соответствующие значения можно ввести вручную. Кроме того, программа может выполнить автоматический расчет путем интерполяции по методу наименьших квадратов.
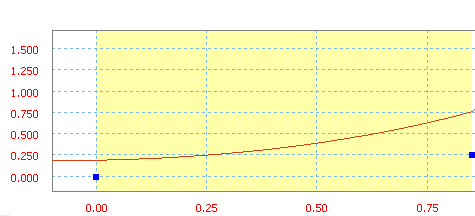
Полином, где a0=20 дюймов, a1=10 дюймов/с, a2=50 дюймов/с² и a3=20 дюймов/с³.
Сплайн	значение уклона линии. Сплайн - кубическая функция, интерполируемая между двумя последовательными точками. Существует несколько способов определения сплайна. а именно: Точки ввода можно быстро определить, дважды щелкнув или щелкнув правой кнопкой мыши в области графика и выбрав пункт "Добавить точку". Однако программа воспринимает этот сектор как последовательность секторов, а не как единый сектор кривой. Для более точного ввода координат необходимо импортировать текстовый файл. Исходный уклон - задание уклона первой точки. Конечный уклон - задание уклона конечной точки. Можно загрузить ранее определенный сплайн.
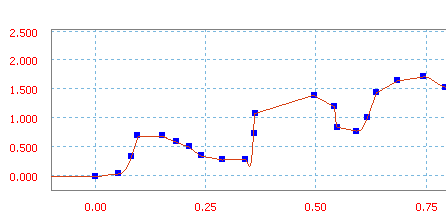
Сплайн, определенный путем добавления точек.
Определяемый сплайн можно сохранить здесь, независимо от способа его определения. Прим.: для сектора, определенного с помощью сплайна, нельзя добавить другие формулы. Кроме того, при замене формулы сектора сплайном исходный и конечный уклоны определяются автоматически на основе предыдущего и последующего секторов. Впоследствии эти настройки можно изменить.
если требуется использовать текстовый файл, содержащий точки касания, структура файла должна быть следующей:
// комментарии	В файл можно добавить одну или несколько строк в качестве пояснений. Каждая строка должна открываться двойной косой чертой “//”. Строки пояснений не обязательны для заполнения, однако в них можно указать назначение сплайна.
[Касательные] T1 T2	Укажите значения для угла наклона касательной в начальной (T1) и конечной (T2) точках сектора. Эти значения отображаются в интерфейсе пользователя как уклон "в начале" и "в конце". Если значение не указано, для угла наклона касательной используется значение 0,0 (горизонтальная касательная). Эта строка также не является обязательной для заполнения, однако, если значение угла наклона касательной не указывается, следует принять некоторые допущения.
X₁ Y₁ ... X_n Y_n	список координат точек, можно указывать любое количество точек. Определите одну точку для каждого ряда.
Образец текстового файла	// // Исходные точки сплайна, указываемые для моделирования // Значение: Вращательный момент в соединении (Н мм) // Опорное значение: время, с [Касательные] -3,40775 -5,27803 +0,000 +0,000 +4,313 +1,510 +7,954 -9,756 +1,000 +0,000
Формула	формула для определения кривой. Формула - это уравнение с функциями и ключевыми словами. Доступно только для описания соединения и внешних сил. Нельзя применить движение к степени свободы. Целостность с граничащими секторами не сохраняется автоматически. Их необходимо определить во избежание возникновения конфликта во время моделирования. Длина формул ограничивается 255 символами. Можно использовать любую из ниже перечисленных функций. abs fmod a cos cos log10 sqrt asin sinh log sqr atan sin pow trunk atan2 tanh Знак pow10 floor cosh tan sign0 exp round
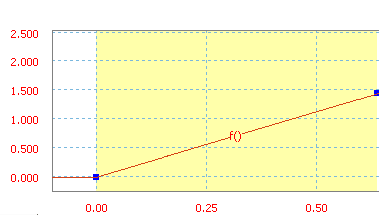
Кривая определяется формулой Y = X + 37,

Пример 1

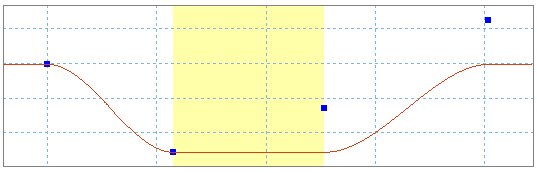
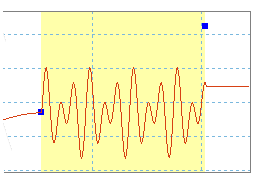
Допустим, требуется создать три сектора. Во втором секторе создадим синусоиду низкой частоты.

На рисунке изображена кривая до и после создания синусоиды. Третий сектор сместился вертикально, обеспечив непрерывность между двумя секторами. Для получения нужной кривой необходимо добавить дополнительные функции.

Пример 2

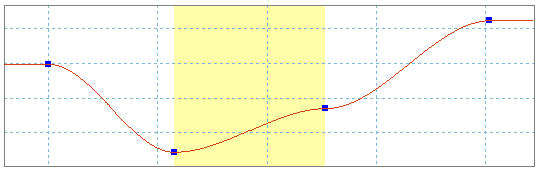
Для отдельных функций возможность определения ограничена. Чтобы получить функцию, изменяющуюся по закону синуса относительно значения 300, необходимо сложить постоянную функцию со значением 300 с функцией синуса.

Прим.: Порядок добавления функций не имеет значения.

Отклонение вблизи ненулевого наклона можно смоделировать в виде сочетания наклонной прямой и синуса.

Пример 3

Для моделирования вибрации колебательного движения необходимо сложить синусные функции с различными амплитудами и частотами.

Задание значений за пределами сектора кривой

Интересно проследить поведение переменной за пределами секторов кривой: перед первым и после последнего сектора. После выбора области за пределами всей кривой и добавления необходимых условий можно приступить к описанию выбранной области.

Выберите описание для выбранной области за пределами кривой.
Если выбрано значение "Циклическая", нажмите кнопку "Старт".
Откроется диалоговое окно "Выбор начальной точки".
В диалоговом окне "Выбор начальной точки" щелкните стрелку вниз, расположенную справа от поля.
В открывшемся меню отобразятся все начальные точки секторов кривой.
Щелкните начальную точку сектора кривой, которую требуется скопировать для данной области.
Нажмите "OK".

Существует пять вариантов описания области за пределами кривой. а именно:

Постоянное значение	При выборе данного параметра задается постоянная величина в качестве первого значения кривой (в случае описания области слева от первой точки) или в качестве последнего значения кривой (в случае описания области справа от последней точки). Данный параметр установлен по умолчанию.
Постоянный уклон	При выборе данного параметра задается отрезок постоянного уклона в описываемой области. Значение уклона равно либо значению уклона первого сектора кривой (в случае описания области слева от первой точки), либо значению уклона последнего сектора кривой (в случае описания области справа от последней точки).
Модуль	При выборе данного параметра задается значение в области определения формулы (все секторы выбраны) в соответствии с модульным принципом, т.е. описываемая кривая повторяется с обеих сторон оси ординат. При динамическом моделировании проверяется соответствие ординаты последней точки формулы (последний сектор) ординате первой точки (первый сектор). В случае несоответствия отображается сообщение об ошибке с запросом на изменение значений. Это сообщение отображается потому, что расчет не работает в случае прерываний. Данный режим применяется для правой и левой частей формулы.
Циклическая	В этой функции используется копия цикла, начинающегося с пользовательской точки и заканчивающегося последней точкой пользовательской кривой. Для обозначения начала цикла необходимо выбрать точку, соответствующую последней точке на пользовательской кривой. Иначе возможен разрыв между начальной и конечной точками цикла. В случае разрыва отобразится сообщение об ошибке.
Произвольно	При выборе данного параметра описание для области не задается. Сила не прикладывается, и вынужденное движение в этом направлении, заданное для степени свободы становится свободным. Для вынужденного движения, перед тем как задать свободное движение для последнего сектора, необходимо задать свободное движение для сектора справа от последней точки, затем для предпоследнего сектора и т.д.