小变形分析是最常见的分析类型,是大变形分析和挫曲分析的基础。深入了解小变形分析是了解其他类型分析的重要前提。
小变形分析也常常被称为线性分析。
假设
小变形分析基于如下假设:通过向柔体施加载荷而产生的位移以及相应的应力和应变是此类载荷大小的线性函数。
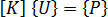
其中:
-
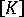 是理想化结构的组合刚度矩阵,
是理想化结构的组合刚度矩阵, -
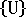 是未知的节点位移向量,
是未知的节点位移向量, -
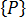 是相等节点作用力的向量。
是相等节点作用力的向量。
本构模型
在线性弹性材料(遵守胡克定律的材料)条件的限制范围内,仍可能同时包含均质和非均值材料。但在这种情况下,对于薄壳单元(LMT3、LBT3),假设材料在厚度方向上是均质的。在此限制下,结构中各个点的材料属性各不相同,但在每个点,都存在弹性模量取主要值(即最大值和最小值)所相关的两个正交方向。这些方向称为正交方向,相关的材料模型称为正交模型。
有两种弹性材料模型可供选择。第一种是各向同性模型(材料无方向且均质)。第二种是上述特殊情况的正交模型,其中,主模量值的任何点到点变化均被忽略(材料为多向且均质)。后一种模型适用于模制塑料,因为它在成型工艺中会考虑出现的分子取向影响。
边界条件
在应用边界条件之前,平衡等式是单一的,即,刚度矩阵 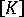 为非正定并且不可逆。但是,通过应用一组适当的位移边界条件可以正定渲染刚度。如果删除所有可能的刚体位移模式,得出的“减小的”等式集将被确定(即
为非正定并且不可逆。但是,通过应用一组适当的位移边界条件可以正定渲染刚度。如果删除所有可能的刚体位移模式,得出的“减小的”等式集将被确定(即 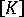 为正定)。实际上,如果有限元模型免于内部释放(例如顶针),并且单元本身不包含任何伪零能模式,则任何为结构的六个可能刚体移动提供有限(大于零)阻力的位移约束集都是可以接受的。
为正定)。实际上,如果有限元模型免于内部释放(例如顶针),并且单元本身不包含任何伪零能模式,则任何为结构的六个可能刚体移动提供有限(大于零)阻力的位移约束集都是可以接受的。
为了给可用的位移约束形式分类,假定受约束的节点处与各个自由度对应的运动受到外部(与地连接)弹簧的阻力,这种假设很有用。三种最常见的位移边界条件为:
-
刚性(位移为零,弹簧刚度无限大)。
-
半刚性(位移非零,弹簧刚度有限)。
-
规定(位移为规定的非零值,无弹簧)。
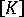 必需的主对角线系数
必需的主对角线系数 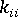 替换为系数
替换为系数 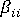 ,该系数足够大,可将约束等式从剩余集中分离。同时,第 ith 个分量(作用力向量
,该系数足够大,可将约束等式从剩余集中分离。同时,第 ith 个分量(作用力向量 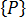 的)应设置为零。后一种技术可以很容易地扩展到规定位移的情况,只须将第 ith 个分量(
的)应设置为零。后一种技术可以很容易地扩展到规定位移的情况,只须将第 ith 个分量( 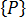 的)设置为:
的)设置为: 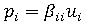
其中 是所需位移。保留完整(原始)等式集的好处在于:在倒转代换阶段,计算受约束节点处的反作用所需的信息可直接使用。
施加的载荷
广义的载荷术语 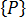 被称为等效载荷向量,因为它表示分布式载荷(例如压力、牵引力、实体作用力、初始应变或初始应力)以及直接施加到节点的集中载荷。在前面的情况中,总是能发现节点作用力系统与指定的分布式载荷相平衡。对于简单单元,这些作用力将与施加的载荷静态相等(即只能从静态平衡条件中找到这些作用力),但在其他情况下,需要详细了解单元公式化才能确定它们的值。任何分布式载荷对
被称为等效载荷向量,因为它表示分布式载荷(例如压力、牵引力、实体作用力、初始应变或初始应力)以及直接施加到节点的集中载荷。在前面的情况中,总是能发现节点作用力系统与指定的分布式载荷相平衡。对于简单单元,这些作用力将与施加的载荷静态相等(即只能从静态平衡条件中找到这些作用力),但在其他情况下,需要详细了解单元公式化才能确定它们的值。任何分布式载荷对 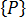 的影响都会由分析自动评估。
的影响都会由分析自动评估。
小变形分析求解
在边界条件和施加的载荷已知后,可通过以下等式获得节点位移 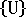 :
:
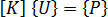
实际上,在对上述等式求解时,对 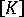 求逆没有必要,且效率低下。相反,应使用高斯消去法对上述等式求解。
求逆没有必要,且效率低下。相反,应使用高斯消去法对上述等式求解。
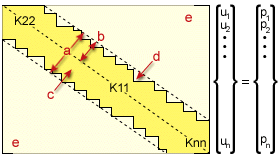
带状刚度矩阵
.(a) 带宽,(b) 半带宽,(c) 轮廓,(d) 轮廓线,(e) 带外全部为零。
刚度矩阵 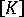 具有三个可以使高斯消元法非常有效的属性:
具有三个可以使高斯消元法非常有效的属性:
-
矩阵是对称的(即,主对角线一则的条目是另一侧的“镜像”)。主对角线是从左上角到右下角条目的假想线。
-
矩阵中的大多数项为零。
-
在矩阵中,所有非零项都位于以主对角线为中心的狭窄带内。
带状刚度矩阵展示了刚度矩阵的外观。(大多数)非零项和所有零项之间的边界称为轮廓线。主对角线和轮廓线之间的系数集称为轮廓。由于矩阵 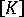 呈带状且稀疏,仅在轮廓内执行消元可缩短处理时间。而
呈带状且稀疏,仅在轮廓内执行消元可缩短处理时间。而 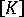 的对称性进一步减少了运算量,因为部分要消去的
的对称性进一步减少了运算量,因为部分要消去的 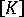 在消元的任何阶段都保持对称,因此无需计算已知的对称项。
在消元的任何阶段都保持对称,因此无需计算已知的对称项。
为了使效率最大化,应首先使用节点重新编号方案将轮廓内系数的数量最小化(重新编号操作对用户完全透明)。所采用的带宽优化算法来源于 Gibbs、Pool 和 Stockmeyer [1]。
分析中涉及的等式数量通常过多,以致于无法在虚拟内存中拟合所有系数(由于历史原因,我们称虚拟内存为““核心””)。为求解此类大型等式组,将使用一个““核心外””求解器,其中完整矩阵保存在二级存储器(通常为硬盘驱动器)中。这样,如有必要,完整矩阵会被分成多个块,在任何一个时间只对““核心””中的两个块执行高斯消元(当一个块包含耦合系数时缩减另一个块)。最小块大小等于以下变量的最大半带宽: 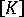 。最大块大小与机器相关,但程序会自动指定适合于获得最高效率的值(最高效率通常与使用最小数量的大型块相符)。
。最大块大小与机器相关,但程序会自动指定适合于获得最高效率的值(最高效率通常与使用最小数量的大型块相符)。
多载荷情况
应力和翘曲分析可为分析指定多种载荷情况,即不同的收缩应变或外部载荷情况。这些多载荷情况可以非常高效地解决,因为结构刚度矩阵 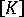 已经过一次公式化,然后又用于确定每种载荷情况的位移
已经过一次公式化,然后又用于确定每种载荷情况的位移 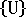 。每种载荷情况都会显示为作业进度表中的一行,该作业进度表将写入分析的结果文件。
。每种载荷情况都会显示为作业进度表中的一行,该作业进度表将写入分析的结果文件。
分析输出
位移场已知后,每个单元的应变-位移和应力-应变关系都将用于确定单元内不同位置的应变和应力级别。在 FENAS 中,这些位置将被自动选择,以便在对单元体积进行积分以确定单元刚度矩阵时,它们与所使用的数值积分位置相符。用作数值积分位置的应力/应变恢复点是最优或接近最优的。
除了回应输入数据外,分析输出文件还包含受约束节点和最初移位节点处的反作用力、节点位移和单元应力。
按照定义,所有这些量均是所施加载荷的线性函数,因此,如果负载被减半,位移和应力也将被减半。这样便可随意选择任意名义强度的载荷,而不会影响结果的性质有效性。但是,当扩展此概念以包含材料常数的影响时必须十分小心。如果结构由外部施加载荷,应变和位移将与材料常数成反比例关系(对于正交材料来说,为了维持比例,必须保持材料模量常数的比率),但应力将保持不变。另一方面,如果不受约束的结构受到““内部””载荷(例如由温度变化或自由收缩引起),则应力将与材料的机械属性成比例关系。位移将保持不变。最后,对于涉及内部和外部载荷的问题,位移和应力都取决于材料模量。
结果诠释
在获得首个小变形解后,建议执行的流程是检查结果是否合理。最佳方法是详细查看位移场。使用图形化的后处理工具可轻松完成此操作。
需要问的问题有:
- 图案看起来是否合理?
- 大小是否大致符合预期?
- 是否有任何期望的对称性被复制?一般来说,仅当几何、载荷和边界条件均对称时才能复制对称性。请注意,如果有限元网格本身不对称,则结果中任何期望的对称性都几乎无法准确复制。
但您对获得了一致的位移场以及平均应力级别相对于指定的材料数据和其他参数很合理而感到满意后,需要决定是否应使用更精细的网格进行第二次分析。通常需要使用两种不同的网格密度进行求解的原因很简单,是因为有限元方法始终会得到一个准确或完全收敛的解的近似值。言下之意,只有通过查看两种网格结果中发生的变化才能达到客观的准确度测量。
进一步阐述这个重点,在应力分析中,假设您希望 von-Mises 应力的预测峰值级别至少达到 95% 的准确度,并且已获得该应力对应于两种不同网格的两个值。如果对应于两种网格的应力的变化小于 5%,假设从该点的收敛为单调收敛(如果目标准确度大致在 95%-100% 的范围内,通常将是这种情况),则说明较精细网格的结果超出了目标准确度。另一方面,如果变化大于 5%,则必须使用更精细的网格并重复该过程,直至达到目标为止。请注意,当只有两种网格的解为已知并且较精细的网格通过测试时,不能判断出较粗糙的网格是否也通过测试(要回答此问题,必须分析比最初两个网格更粗糙的第三个网格)。
在此背景下,应该清楚实际只有一种情况可认为第二个更精细的网格的解没有必要。即是您已经从以前类似问题的有限元分析中积累了足够的经验,并确信您所使用的网格可满足所需的准确度。
小变形分析的相关性
小变形(相对于大变形)分析本身能成为有价值的工具有三个主要原因:
-
对于结构机械特性的有用和一致信息的获取,小变形分析提供了最快和最有效的方法。
-
小变形分析为了解和深入理解范围广泛的““结构机械””问题提供了极佳工具。此外,在对小变形响应有一定了解之前,您完全无法理解相应的大变形响应。
-
在决定网格密度和网格分布方面,小变形分析提供了唯一经济实惠的方法。由于非线性分析可以被看作一系列线性化步骤,且其中每个步骤都由不同的起始条件集决定,通常认为在小变形收敛研究基础上进行的准确度检查在大变形范围内也近似有效。
参考
1. Gibbs, N.E., Poole, W.G., and Stockmeyer, P.K., “An algorithm for reducing the bandwidth and profile of a sparse matrix”, S.I.A.M. Journal on Numerical Analysis, Vol. 13, No. 2, 1976, pp. 236-250。