实际上,大多数结构将仅在限制的载荷强度范围内显示线性响应或近似于线性的响应。在较高载荷处,结构的刚度可能发生显著的变化,从而导致非线性响应。
举一个简单但实际的非线性示例,假定一个长度为 L 的细长柱在顶端受到一个水平力 H 和一个向下的垂直力 V(柱底端被夹紧,顶端不受约束)。若忽略顶尖向下的微小移动,此类载荷系统的主要影响是使柱的顶部产生一定量的侧向偏移,将该偏移量设为 u。如果现在考虑该位移配置中的结构和载荷,则可立即得到柱底部的弯矩 M:
M = HL+Vu
M 不仅是外部载荷的函数,还要取决于 u,这直接说明了问题是非线性的。显然,作用在弯曲柱上的垂直载荷作用将会进一步增加侧向位移,因此无法直接对问题进行求解。但可以通过将施加的载荷 H 和 V 划分成微小增量,然后逐步将载荷增加到所需级别来接近真解。
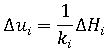
- i 是增量编号
- ki 是柱顶尖的当前侧向刚度。
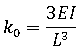
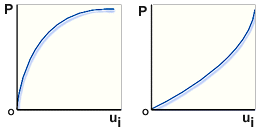
非线性响应的载荷-位移图
.左侧软化响应,右侧硬化响应,P 非线性载荷,ui 位移图
在上面的示例中,我们使用了跟随非线性载荷-变形路径的近似方法。在此方法中,只能采用无穷小的步才能找到真实或准确的响应。为了理解非线性响应的更准确模型的基础,需要认识到结构在真载荷-变形路径上的每个点都必须保持平衡状态。事实上,真正的情况是随着载荷的增加,结构会呈现由平衡唯一决定的连续配置。因此,在载荷-位移空间中绘制的任何曲线都可以更准确地称为平衡路径。在含有多个自由度的结构中,刚度矩阵的各种系数会随着载荷强度的变化而以不同的速率变化。因此,按照施加的载荷绘制不同的位移分量而获得的平衡路径可能有很大不同。适合于绘图的分量的选择看起来是随意的,但其实是强制的,因为完全(普遍的)非线性响应实际会在 (N+1) 维载荷-位移空间中产生一个面(其中 N 是结构的自由位移度数)。
平衡等式

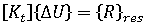
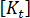 是当前配置的线性刚度矩阵。
是当前配置的线性刚度矩阵。 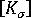 是当前配置的初始应力或几何刚度矩阵。
是当前配置的初始应力或几何刚度矩阵。 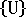 是增量节点位移的向量。
是增量节点位移的向量。 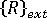 是等于当前级别外部施加载荷的节点作用力的向量。
是等于当前级别外部施加载荷的节点作用力的向量。 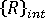 是等于内部应力场的节点作用力的向量。
是等于内部应力场的节点作用力的向量。 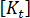 是当前配置的正切刚度矩阵。
是当前配置的正切刚度矩阵。 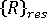 是当前配置中残余(非平衡)节点作用力的向量。
是当前配置中残余(非平衡)节点作用力的向量。
这些等式为非线性,无法直接求解。我们可以改用经典的预测校正迭代技术(例如,牛顿-拉弗森法或拟牛顿法),其中左侧用作预测器,右侧用作校正器。在一组正常的(成功的)迭代循环中,结构的配置将向真实的平衡配置收敛,同时残余的不平衡力 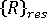 将变为任意小。实际上,达到一个目标精度(由程序或用户定义)后,迭代就会终止。请注意,在平衡迭代期间,载荷级别通常保持不变。
将变为任意小。实际上,达到一个目标精度(由程序或用户定义)后,迭代就会终止。请注意,在平衡迭代期间,载荷级别通常保持不变。
求解方法
- KSTRA=0:初始刚度法
-
此方法成本很低但相当粗糙,其中初始线性弹性刚度
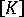 用于所有载荷增量以及增量内的每个迭代循环(初始刚度法)。由于位移增量的预测始终基于以初始几何为基础的刚度矩阵线性化,收敛非常缓慢,并且只要在平衡路径中遇到任何明显的非线性特征,算法通常就会失败(即,规定数量的迭代内发生分歧或收敛失败)。
用于所有载荷增量以及增量内的每个迭代循环(初始刚度法)。由于位移增量的预测始终基于以初始几何为基础的刚度矩阵线性化,收敛非常缓慢,并且只要在平衡路径中遇到任何明显的非线性特征,算法通常就会失败(即,规定数量的迭代内发生分歧或收敛失败)。 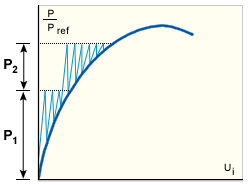
初始刚度法
- KSTRA=1:改进的牛顿-拉弗森法 (MNR)
-
此处结构刚度矩阵已更新并在每个载荷增量的起始点分解,即在前一步结束时得到的平衡配置(用于软化结构的改进 NR 法和用于硬化结构的改进 NR 法)。然后在不改造刚度的情况下进行迭代。该策略非常适合于平衡路径中略微非线性的部分。
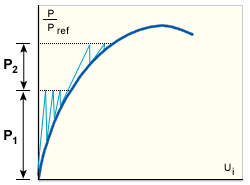
用于软化结构的改进 NR 法
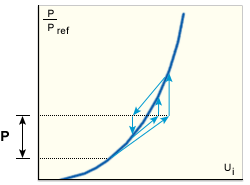
用于硬化结构的改进 NR 法
- KSTRA=2:NR 法与 MNR 法组合
-
此方法是修改的 MNR 法,其中,在步骤开始时和第一次迭代之后对刚度进行改造和分解(用于硬化结构的组合法)。此算法可处理中等非线性。
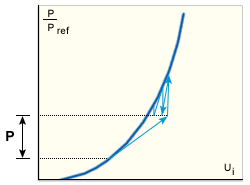
用于硬化结构的组合法
- KSTRA=3:牛顿-拉弗森法 (NR)
-
在此方法中,结构刚度矩阵在每个迭代循环开始时更新(完整 NR 法)。该方法体现出快速(接近二次)收敛的特点,适用于处理平衡路径中较强的非线性和分叉。但是,对于给定数量的迭代,它显然是目前最耗时的方案。
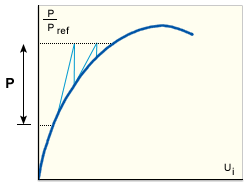
完整 NR 法
- KSTRA=4:减小步长的牛顿-拉弗森法 (NR)
-
此策略与 KSTRA=3 相同,引入该方法的目的是当使用 KSTRA 3 遇到收敛困难时,重新采用四分之一步长的步,同时保持纯 NR 迭代。
- KSTRA=5:载荷步进
-
在此方法中,平衡迭代被暂时抑制。因此,对于每个载荷增量,只需要改造和减少一次结构刚度,并且不使用迭代(直接载荷步进)。为了将与真实平衡路径的偏移最小化,载荷增量必须远小于 MNR 或 NR 中使用的载荷增量,并且必须将不平衡力移入下一步(而不是丢弃)。仅当所有其他策略均失败时才使用该方法。
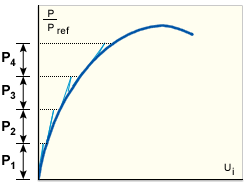
直接载荷步进
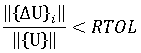
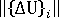 是两个连续迭代间节点位移变化的欧几里得范数,即:
是两个连续迭代间节点位移变化的欧几里得范数,即: 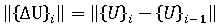
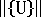 是当前总节点位移的欧几里得范数。要使用的适当的 RTOL 值在某种程度上与问题相关,但位于 0.01 至 0.0001 范围内的值预计可以提供足够的精度。
是当前总节点位移的欧几里得范数。要使用的适当的 RTOL 值在某种程度上与问题相关,但位于 0.01 至 0.0001 范围内的值预计可以提供足够的精度。 自动控制技术
非线性有限元分析的主要难题之一是没有单个迭代方法可完全适合于整个解路径。当路径的非线性更加严重时,所选策略可能会收敛失败,而导致无法取得进一步进展。显然,需要一个能够使用不同的步长和/或不同的策略来重新采用已失败步的自动控制系统。此类方案可用于分析,并已被发现无需干预即可成功地自动跟踪解路径。方案的特点如下:
- 选择一个初始最小策略(通常 KSTRA=1 或 2)和一个初始步长。该策略将保持到遇到收敛困难(如果有)为止。
- 在以下情况下,可认为发生收敛困难:
- 在迭代的最大允许次数 Imax内(默认值或由用户指定)未实现收敛,或者
- 解出现分歧(如果对于 4 阶或更高阶迭代,当前位移增量的范数
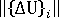 大于步
大于步 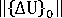 的第一位移增量的范数,则会出现分歧解。非平衡力的欧几里得范数大于所施加载荷的欧几里得范数)。
的第一位移增量的范数,则会出现分歧解。非平衡力的欧几里得范数大于所施加载荷的欧几里得范数)。
- 求解方法按照 KSTRA 值的递增顺序排列。如果遇到收敛困难,程序将使用高一级的策略来重新采用步。同时将步长减小到原来的四分之一。新策略将保持,直到再出现收敛困难,此时将选择更高一级的策略并再次减小步长。
- 该过程将持续至达到最大步数或者载荷超过允许级别(这两个参数都可以由用户调整)。
- 一旦所使用的策略的级别高于初始选择的策略,在以下情况下将尝试回到低一级的策略:
- 当前策略(KSTRA = 1、2、3 或 4)的四个步骤不需要多于允许次数一半的迭代次数,或者
- 当前策略 (KSTRA = 5) 已使用四次。
如果所选的较低级别的策略失败,则前一个方法将被用于后续的四个增量,但不会额外减小步长。
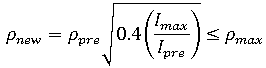
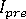 是前一步使用的迭代次数,
是前一步使用的迭代次数, 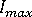 是最大迭代次数,
是最大迭代次数, 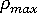 是步长极限(可由用户调节)。举例说明,假定
是步长极限(可由用户调节)。举例说明,假定 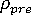 = 1,
= 1, 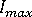 = 20,
= 20, 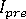 = 4,并且
= 4,并且 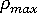 = 2。则根据公式可确定当前步长为
= 2。则根据公式可确定当前步长为 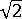 。
。 这也说明,在收敛失败后,将在四个步骤(每个步骤平均 4 次迭代)后恢复原始步长(即,失败的增量中使用的步长)。请注意,当 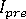 超过
超过 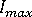 的 40% 时,步长将会缩小,尽管相对较慢。
的 40% 时,步长将会缩小,尽管相对较慢。