對於自由度極少的問題而言，在給定 N 階 多項式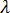 
(N 是不受限制的自由度數目) 的情況下，可以明確求出行列式的值。
將會有 N 個實根，而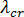 
將等於這些根中的最小值 (在大小上)。將 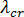重新代入到挫曲方程式將會得出臨界挫曲位移模式。會將此模式定義為任意縮放的一組位移，對應於在挫曲期間發生的構形變化。因此，如果我們希望檢視結構的後挫曲構形，必須在結構的未變形構形上加上與 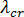相關的臨界位移模式。
針對具有許多自由度的結構，在多項式展開之後使用開方根方法會變得不可行。若要使用更一般的求解演算法，必須用廣義特徵值問題來識別挫曲方程式。與此特徵值問題相關的，有 N 個實數特徵對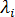 
、 
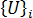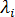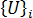，其中 i = 1,...N， 與 分別是代表第 ith 個臨界負載係數與挫曲位移模式的第 ith 個特徵值與特徵向量。您可以使用功能強大而一般目的性的方法來求解廣義特徵值問題。所使用的方法稱為子空間迭代方法 [1]。
使用子空間迭代方法，我們可以求出一系列 (例如 n 個) 依 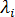的大小遞增排列的特徵對，亦即 
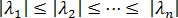，在此之後是 = 
， 
= 。
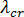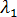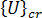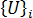所要求出的特徵值數是您可在「翹曲」或「應力」分析中指定的參數。但是請注意，隨著所需特徵對解數的增加，所需的計算量也會明顯增加。此外，在挫曲問題中，我們通常只對"「實數」臨界狀態感興趣，而不會對假定較高順序的模式感興趣。"儘管並不常見，在增加的負載下，若要使結構從第一臨界模式變更 (通常透過分歧) 為其他較高順序的模式，假設對應於後一種模式的負載等級與挫曲形狀在意義上與預測的第一模式相關，這是相當錯誤 (及危險) 的。原因是，在從較低挫曲模式轉換為較高挫曲模式的過程中，結構的構形很可能會遭遇重大的變化，因此與挫曲分析的基本假設之間產生了明顯的衝突。
預測特徵值正負
請注意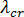， 的值沒有限制，正值、負值都可以接受。因此，舉例來說，如果選取 
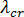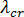而使它在平板中產生了抗拉應力場，則 將為負。另一方面，反轉 的方向，使應力狀態受到壓縮，將使 為正值。但是，依照定義，兩個 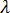值的大小將完全相同。如果反轉參考負載 ，實際上便足以單獨求出第一個特徵對 (這會在之後發生，因為我們知道當 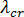為負時，反轉 的方向將只會反轉 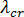的正負)。但是，當我們考慮不可恢復的負載系統時，便會發生困難。在此情況下，挫曲將對應於最低的正特徵值，且由於不可能事先分辨有多少負特徵值，因此我們必須進行反覆試驗，或進行單一分析，在其中要求至少兩個特徵對。到目前為止對於不可逆轉負載系統 (例如對塑膠元件產生作用的收縮應變) 的經驗指出，前兩個特徵對的解通常便已足夠 (亦即兩個 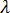值都為正，或一個為負，一個為正)。
Sturm 序列檢查
使用子空間迭代方法，偶爾可能會跳過一或多個特徵值，因為在預測值中可能會遺失實際存在的一或多個特徵值。因此，可以使用一種叫做 Sturm 序列檢查的技巧來檢查遺失的特徵值。不幸的是，n 個特徵值中如果有任何一個為負，則檢查便無效。
挫曲結果的有效性
當執行挫曲分析時，請務必記住初始假設的限制特性。如果在挫曲之前形狀發生重大變化，結果將變得不可靠，因為方法是在有效性的範圍之外應用的。通常，這表示將會過度評估 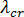，但並非始終如此。如果有理由相信結構的預挫曲位移不小，則始終應在挫曲分析之後執行完整的大型撓曲分析。
挫曲類型
-
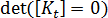
限制點。
-
分歧。
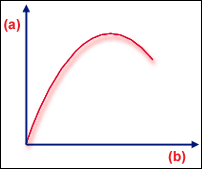
限制點
.(a) 負載，(b) 撓曲
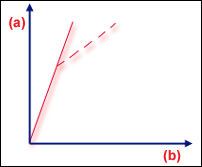
完美結構的分歧
.(a) 負載，(b) 撓曲
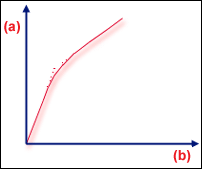
實際結構的分歧
.(a) 負載，(b) 撓曲
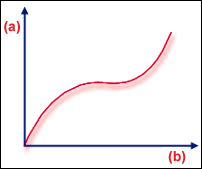
先軟化再硬化
.(a) 負載，(b) 撓曲
不嚴格地說，限制點是元件在形狀無主要變化的情況下，無法再接受更多負載的狀態 (限制點)。這通常會在圓頂狀的元件中發生，其中心負載可能會導致圓頂"失穩"。更普遍的情況是，當在挫曲點之前存在明顯的幾何非線性時，我們會預期挫曲屬於限制點類型。在圓頂範例中，元件需要變得相當平坦，勁度矩陣多項式才能變為零。在"「失穩」(可能比較輕微或很嚴重) 之後，元件將可接受更多負載，但一般而言，必須將元件設計為使預期負載不會達到限制點。"
分歧是一個"「分支」點，其中的兩個可能的平衡狀態彼此很接近。"如果您想要一個完美對稱的平板，則板對平面內壓縮負載的回應會是線性的。但是，當負載超出臨界值時，平衡會變得不穩定；就像山頂上的球一樣，不知道會從哪個方向滾下來。因此實際平板將會在臨界負載等級挫曲。因此我們有兩個可能的平衡路徑，我們將其交點稱為「分歧點」""(完美結構的分歧)。
在翹曲或熱負載問題中都可能會發生這兩種挫曲，但分歧比較常見。在平板範例中，板中的瑕疵會導致分歧點的勁度急遽變化變得平緩 (實際結構的分歧)。另一個常見的回應是「先軟化再硬化」""(先軟化再硬化)。在此情況下，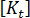 
的多項式會降至某個較小值，但不是零。
情況的挫曲分析，如完美結構的分歧和實際結構的分歧通常可以明確指出分歧位置。限制點之類的情況分析傾向於過度預測限制點。在先軟化再硬化之類的問題中，並沒有明確的挫曲負載，但挫曲分析通常將會指出非線性從何處開始變得嚴重。
參考文獻
1. Bathe, K.J., Finite Element Procedures in Engineering Analysis, Prentice-Hall, Englewood Cliffs, New Jersey, 1982, pp. 666-696.