儘管依照結構回應的完全非線性增量/迭代方法非常普遍且相對精確,但也可能要花費大量的時間進行計算。
由於挫曲的基本重要性,及其設計意圖,如果有一種簡化的方法,能夠提供臨界負載等級的逼近,並預期會在此處發生挫曲,這很明顯的會很有價值。經過證明,如果我們假設預挫曲回應為線性,且預挫曲位移的影響無關緊要,便可設計此類方法。這種我們稱之為挫曲分析的方法,又稱為初始穩定性或傳統分歧分析。
以下部分描述一般性挫曲分析方法及該分析所使用的兩種特定方法。
一般性挫曲分析
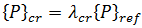
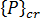 為已套用負載分佈的臨界層級,
為已套用負載分佈的臨界層級,  為相同負載分佈 (參考負載) 的任意層級,
為相同負載分佈 (參考負載) 的任意層級, 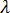 為純量乘數。
為純量乘數。
在這些定義之下,挫曲會在負載乘數 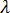 達到臨界值
達到臨界值 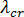 時發生。挫曲分析的起點是假設勁度矩陣的每一個係數
時發生。挫曲分析的起點是假設勁度矩陣的每一個係數 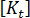 都會隨著套用的負載產生線性變化。如上所述,我們可以將套用的負載想像為某個參數 (例如
都會隨著套用的負載產生線性變化。如上所述,我們可以將套用的負載想像為某個參數 (例如 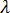 ) 乘以力的常數向量
) 乘以力的常數向量  。
。
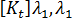 和
和 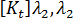 ),以及我們對於線性的假設,任何特定平衡構形的勁度矩陣
),以及我們對於線性的假設,任何特定平衡構形的勁度矩陣 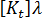 由以下方程式得出:
由以下方程式得出: 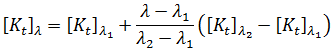
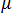 ,且勁度從
,且勁度從 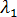 變為
變為 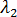 (為
(為 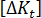 ),則:
),則: 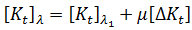
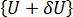 ,都位於相同的負載層級。
,都位於相同的負載層級。 如下圖所示,其中展示挫曲的兩個基本類型的平衡構形 (稍後會更加詳細地討論)。
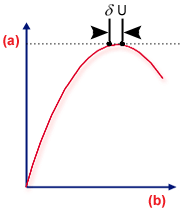
限制點
.(a) 負載,(b) 撓曲
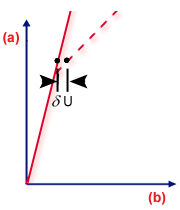
分歧點
.(a) 負載,(b) 撓曲
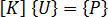 ,我們可以這樣寫:
,我們可以這樣寫: 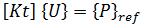
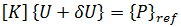
 表示兩個平衡構形之間的無窮小位移。從第二個方程式中減去第一個方程式可得出:
表示兩個平衡構形之間的無窮小位移。從第二個方程式中減去第一個方程式可得出: 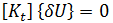
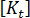 是
是 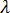 的函數。從線性代數中,我們得知求以上方程式的解即等於求以下方程式的解:
的函數。從線性代數中,我們得知求以上方程式的解即等於求以下方程式的解: 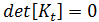
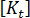 的多項式為零時發生。因此,針對一般性挫曲問題求解的方程式為: 這是特徵值問題,其中的 是要求得的未知數。以上方程式可透過標準方法 (例如子空間迭代) 來求解。
的多項式為零時發生。因此,針對一般性挫曲問題求解的方程式為: 這是特徵值問題,其中的 是要求得的未知數。以上方程式可透過標準方法 (例如子空間迭代) 來求解。 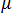 的定義,我們得出:
的定義,我們得出: 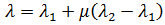
線性 (傳統) 挫曲分析
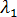 = 0,且
= 0,且 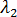 = 1,亦即使用零與完全套用的負載做為參考狀態。在此情況下,
= 1,亦即使用零與完全套用的負載做為參考狀態。在此情況下, 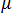 會減少為
會減少為 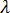 ,且方程式會變為:
,且方程式會變為: 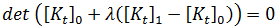
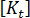 分成兩個分量:
分成兩個分量: 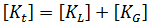
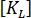 是一級勁度矩陣,而
是一級勁度矩陣,而 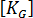 是較高級的勁度矩陣 (又稱為應力或幾何矩陣)。
是較高級的勁度矩陣 (又稱為應力或幾何矩陣)。 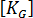 是材料應力的線性函數
是材料應力的線性函數 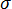 。
。 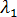 = 0 表示
= 0 表示 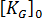 = 0。因此:
= 0。因此: 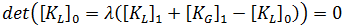
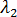 = 1 為止的回應純粹為線性,亦即將使用原始座標計算應力與
= 1 為止的回應純粹為線性,亦即將使用原始座標計算應力與 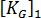 。使用傳統方法做出的另一假設為,勁度的一級零件不會隨負載改變,亦即
。使用傳統方法做出的另一假設為,勁度的一級零件不會隨負載改變,亦即 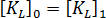 。在完全 Lagrangian 術語中,這等同於忽略所謂的「位移矩陣」影響。""因此以上方程式會減少為:
。在完全 Lagrangian 術語中,這等同於忽略所謂的「位移矩陣」影響。""因此以上方程式會減少為: 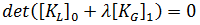
線性挫曲方法可用於非以翹曲中之初始條件為基礎的結構或翹曲分析。經驗顯示,翹曲問題的傳統挫曲分析能對挫曲負載做出精確的預測。傳統方法很好用,因為在挫曲之前形狀的變化非常小,亦即 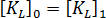 是良好的逼近。
是良好的逼近。
線性化挫曲分析
在此方法中,我們選擇 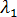 = 0,且
= 0,且 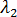 非常接近
非常接近 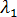 ,亦即使用零與非常小的負載分率做為參考狀態。由於僅採取了非常小的步長,因此不需要平衡迭代,且分析會使用策略 5 執行步長。
,亦即使用零與非常小的負載分率做為參考狀態。由於僅採取了非常小的步長,因此不需要平衡迭代,且分析會使用策略 5 執行步長。
我們也假設 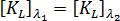 。請注意,在此方法中,應力使用更新的座標計算。
。請注意,在此方法中,應力使用更新的座標計算。
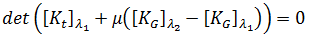
若要分析預先施加應力的元件,最簡單、最快速的方法就是採用 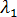 = 0,且
= 0,且 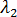 = 0.001。因此只需要採取一個步長,且由於尚未完成平衡迭代,求解的成本只比傳統方法的成本稍微高一點。
= 0.001。因此只需要採取一個步長,且由於尚未完成平衡迭代,求解的成本只比傳統方法的成本稍微高一點。
線性化挫曲方法僅適用於以翹曲分析中的初始條件為基礎的結構分析。無法將傳統方法套用於這些問題,因為製程中有明顯的殘留應力。這違犯了 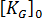 = 0 的假設。因此,必須使用線性化挫曲方法。當您選取初始條件挫曲分析時,這會由應力指出。
= 0 的假設。因此,必須使用線性化挫曲方法。當您選取初始條件挫曲分析時,這會由應力指出。