小型撓曲分析是最常見的分析類型,並且是大型撓曲分析與挫曲分析的基礎。完全瞭解小型撓曲分析是瞭解其他分析類型的一個必要條件。
小型撓曲分析也常被稱為線性分析。
假設
小型撓曲分析的假設基礎為,從負載的應用到彈性本體所產生的位移與對應應力及應變,都是此類負載大小的線性函數。
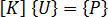
其中:
-
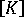 是理想化結構的組合勁度矩陣,
是理想化結構的組合勁度矩陣, -
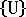 是已知節點位移向量,
是已知節點位移向量, -
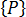 是相等節點力的向量。
是相等節點力的向量。
構成的模型
在線性彈性材料 (符合虎克定律的材料) 的限制之內,仍然可能包含同質與非同質材料。但是,在目前的情況下,對於薄殼元素 (LMT3、LBT3) 來說,我們將假設材料在厚度方向方面是同質的。在此限制之下,材料性質在結構中的一點與另一點之間可能會有所不同,但在每一點上將會有兩個正向性方向,而彈性模數會針對該方向採用主 (即最大與最小) 值。這些方向稱為正向性方向,相關材料模型稱為正向性。
另外還有兩個替代的彈性材料模型。第一個是等向性模型 (材料無方向且為同質)。第二個是如上所述正向性模型的特殊情況,在主模數的值中,任何點對點的變化都將會被忽略 (材料為多方向但為同質)。後者的模型適用於成型塑膠,因為它說明了在成型製程期間發生的分子配向影響。
邊界條件
在套用邊界條件之前,平衡方程式將是奇異的,亦即勁度矩陣 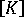 將不會是正定的,而且無法求出其逆矩陣。但是,勁度可以透過套用適當的位移邊界條件組來彩現為正定的。若已移除所有可能的剛體位移模式,所產生的「減少的」方程式組將會是確定數 (亦即
將不會是正定的,而且無法求出其逆矩陣。但是,勁度可以透過套用適當的位移邊界條件組來彩現為正定的。若已移除所有可能的剛體位移模式,所產生的「減少的」方程式組將會是確定數 (亦即 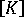 將會是正定的)。實際上,如果有限元素模型可免於內部釋放 (例如銷) 且元素本身不包含任何偽造的零能量模式,則可接受的位移約束組即是為結構的六個可能的剛體移動中的每一個提供有限 (大於零) 阻力的任何一組。
將會是正定的)。實際上,如果有限元素模型可免於內部釋放 (例如銷) 且元素本身不包含任何偽造的零能量模式,則可接受的位移約束組即是為結構的六個可能的剛體移動中的每一個提供有限 (大於零) 阻力的任何一組。
若要為位移約束的可用形式分類,您可以想像在約束節點上對應於每一個自由度的移動都受到外部 (連結至地面) 彈簧的抵抗。因此,位移邊界條件的三個最常見的形式為:
-
剛性 (位移為零,彈簧勁度無限)。
-
半剛性 (位移非為零,彈簧勁度有限)。
-
指定 (位移採用非零指定值,無彈簧)。
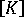 的必要主對角線係數 (即
的必要主對角線係數 (即 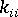 ) 取代為大到足以從剩餘組中取消約束方程式結合的係數 (例如
) 取代為大到足以從剩餘組中取消約束方程式結合的係數 (例如 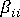 )。同時,應將以下力向量的 ith 分量設定為零:
)。同時,應將以下力向量的 ith 分量設定為零: 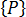 。只需將 ith 分量 (其為
。只需將 ith 分量 (其為 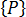 的分量) 設定為以下這樣,便可輕鬆將後一種技術延伸至指定位移的情況:
的分量) 設定為以下這樣,便可輕鬆將後一種技術延伸至指定位移的情況: 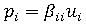
其中, 是所需的位移。保留完整 (原始) 方程式組的優點是,計算約束節點上的反應所需要的資訊可於回代階段中使用。
套用的負載
廣義負載項 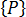 稱為相等負載向量,因為它包括諸如壓力、牽引力、體力、初始應變或初始應力等分佈負載,以及直接套用於節點的集中負載的影響。在前者的例子中,始終可以發現節點力的系統處於與指定分佈負載平衡的狀態下。針對簡單的元素,這些力將靜態地等同於套用的負載 (亦即可單獨在靜態平衡條件中找到這些力),但在其他情況下,必須要對元素公式有詳細的瞭解,才能確定其值。廣義負載項
稱為相等負載向量,因為它包括諸如壓力、牽引力、體力、初始應變或初始應力等分佈負載,以及直接套用於節點的集中負載的影響。在前者的例子中,始終可以發現節點力的系統處於與指定分佈負載平衡的狀態下。針對簡單的元素,這些力將靜態地等同於套用的負載 (亦即可單獨在靜態平衡條件中找到這些力),但在其他情況下,必須要對元素公式有詳細的瞭解,才能確定其值。廣義負載項 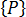 的任何分佈負載的比重都會由分析自動計算。
的任何分佈負載的比重都會由分析自動計算。
小型撓曲分析求解
已知邊界條件與套用的負載時,節點位移 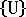 可如下求出:
可如下求出:
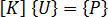
實際上,當求以上方程式的解時,並不需要反轉 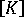 ,這樣做也沒有效果。您可以使用高斯消去法來求以上方程式的解。
,這樣做也沒有效果。您可以使用高斯消去法來求以上方程式的解。
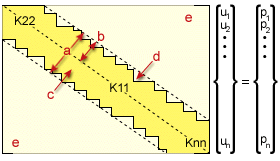
帶狀勁度矩陣
.(a) 帶寬,(b) 半帶寬,(c) 曲線,(d) 天際線,(e) 帶外全部為零。
勁度矩陣 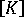 有三個性質,使高斯消去法非常有效:
有三個性質,使高斯消去法非常有效:
-
矩陣是對稱的,也就是說,主對角線一側的項目是另一側項目的「鏡射影像」。主對角線是從左上項目到右下項目的虛擬線。
-
矩陣中的大部分項為零。
-
在矩陣中,所有非零項都位於主對角線周圍置中的窄帶之內。
帶狀勁度矩陣顯示勁度矩陣的外觀。在 (大部分) 非零項與所有零項之間的邊界名為天際線。主對角線與天際線之間的係數組稱為曲線。由於矩陣 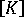 呈帶狀且較為稀疏,因此只需在曲線內執行消去,即可減少處理時間。矩陣
呈帶狀且較為稀疏,因此只需在曲線內執行消去,即可減少處理時間。矩陣 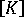 的對稱性會進一步減少計算量,這是因為尚待消除的
的對稱性會進一步減少計算量,這是因為尚待消除的 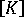 部分在消除的任何階段都保持對稱,因此不需要計算已知的對稱項。
部分在消除的任何階段都保持對稱,因此不需要計算已知的對稱項。
若要獲得最高的效率,曲線內的係數數目會先使用節點重新編號方案減到最低 (重新編號對使用者來說是完全透明的)。所採用的帶寬最佳化演算法由 Gibbs、Pool 與 Stockmeyer [1] 提供。
分析中所牽涉到的方程式數目通常太大,而無法在虛擬記憶體中容納所有係數 (由於歷史的因素,我們將虛擬記憶體稱為「核心」)。""若要對此類大型方程式系統求解,可使用完整矩陣都保存在次級儲存體 (通常為硬碟機) 中的"「核心外」求解器"。因此,如有必要,會將完整矩陣分為區塊及在任何時間僅使用常駐於"「核心」的兩個區塊執行的高斯消去法" (一個區塊會減少,而第二個區塊中包含結合係數)。最小區塊大小等於 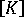 的最大半帶寬。最大區塊大小視機器而定,但會由程式自動指定適合達到最佳效率的值 (最高效率通常與大型區塊最小數目的使用一致)。
的最大半帶寬。最大區塊大小視機器而定,但會由程式自動指定適合達到最佳效率的值 (最高效率通常與大型區塊最小數目的使用一致)。
多重負載的情況
應力與翹曲分析可讓您為分析指定一個以上的負載情況,其為不同的收縮應變或外部負載情況。這些多重負載的情況可以非常有效地求解,因為會對結構勁度矩陣 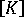 進行一次公式化,然後用來確定每個負載情況的位移
進行一次公式化,然後用來確定每個負載情況的位移 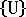 。每個負載情況都會在寫入到分析結果檔案的工作進度表中顯示為一列。
。每個負載情況都會在寫入到分析結果檔案的工作進度表中顯示為一列。
分析輸出
在已知位移場的情況下,每個元素的應變位移與應力應變關係皆可用來確定元素內不同位置的應變與應力等級。在 FENAS 中,將會自動選取這些位置,以使其與求元素體積的積分以求出元素勁度矩陣時的數值積分站一致。使用數值積分站做為應力/應變恢復點是理想或接近理想的。
除了重複輸入資料以外,分析輸出檔案還包括約束及初始位移節點上的反應、節點位移與元素應力。
依照定義,這裡的所有量都是套用負載的一個線性函數。因此,舉例來說,如果負載減半,位移與應力也都將會減半。這可以讓您自由選擇任何標稱負載量,而不會對結果的定性有效性產生影響。但是,當延伸此概念以包含材料常數的影響時,必須特別小心。如果結構在外部負載,應變與位移將與材料常數成反比 (針對正向性材料,要維持比例,將需要保持材料模數的比率恆定),但應力將保持恆定。在另一方面,如果不受限制的結構受到"「內部」負載,例如因溫度變化或自由收縮所導致,應力將與材料的機械性質成比例。"位移將保持恆定。最後,針對牽涉到內部與外部負載的問題,位移與應力都會變得視材料模數而定。
結果說明
當已求得第一個小型撓曲解時建議使用的程序是檢查結果是否合理。執行此動作的最佳方法是詳細檢查位移場。使用圖形後處理功能,將能夠輕鬆達到此目的。
所要提出的問題是:
- 陣列看起來合理嗎?
- 大小程度是您大概預期的程度嗎?
- 是否重新產生任何預期的對稱性?一般而言,此類對稱性只能在幾何圖形、負載與邊界條件全都對稱的情況下重新產生。請注意,如果有限元素網格本身是不對稱的,則將幾乎不會確切地重新產生結果中的任何預期對稱性。
當您對已求出的一致位移場感到滿意時,且平均應力等級在與指定材料資料及其他參數的關係方面有意義時,將必須決定是否需要進行使用較細網格的次級分析。一般而言,為什麼需要對兩個不同的網格密度求解,原因就是有限元素方法始終會導致逼近確切或完全收斂的解。言外之意,只有查看兩個網格結果中發生的變化,才能達到準確度的目標方法。
為了詳述這個重點,在應力分析中,假設您想要在 von-Mises 應力的預估顛峰等級達到至少 95% 的準確度,並求出此應力對應於兩個不同網格的兩個值。如果兩個網格的應力中變化小於 5% ,那麼當假設此點的收斂為單調時 (一般而言,如果目標準確度介於大約 95%-100% 之間的範圍時,就屬於這種情況),便已超出較細網格的目標準確度。另一方面,如果變化大於 5%,則必須使用更細的網格並重複程序,直到達到目標為止。請注意,當只有兩個網格的解為已知狀況,且較細網格通過測試時,是無法確定較粗網格是否也能通過的 (若要回答這個問題,必須分析比原始的一對網格更粗的第三個網格才行)。
就此背景而言,必須認清一點,即實際上只有在一個情況下,才不需要對第二細的網格求解。這個情況就是當您在類似問題的先前有限元素分析基礎上擁有足夠的經驗時,您才能確信您所使用的網格在所需準確度的觀點上是足夠的。
小型撓曲分析的關聯
為什麼小型撓曲 (相對於大型撓曲) 分析就其本身而言是一種高價值的工具,有三個主要的原因:
-
小型撓曲分析提供了最快速、最有效的方法,可以取得有關結構機械行為的實用及一致性資訊。
-
小型撓曲分析提供了優秀的工具,可對"「結構機械」問題的廣泛範圍深入瞭解。"此外,在對小型撓曲回應有一些瞭解之前,您將沒有機會瞭解對應的大型撓曲回應。
-
小型撓曲分析提供了唯一符合成本效益的方法,來決定網格密度與網格分佈。由於可將非線性分析視為一系列線性化步長 (每一個步長都由不同的開始條件組所控制),在小型撓曲收斂研究的基礎上進行的準確度檢查,在大型撓曲範圍中也大致有效,這一點一般是能被接受的。
參考文獻
1. Gibbs, N.E., Poole, W.G., and Stockmeyer, P.K., "An algorithm for reducing the bandwidth and profile of a sparse matrix", S.I.A.M. Journal on Numerical Analysis, Vol. 13, No. 2, 1976, pp. 236-250.