當以遞增方式載入結構時,結構的規劃很可能會在某一負載等級開始較往常更快速地變動。
在相關聯的負載撓曲路徑上,很容易將此項識別為存在斜率與/或曲率明確變化的部分。通常情況下,此類變化將屬於軟化類型,亦即斜率會降低,位移也會比往常更快速地增加,並伴隨著明顯的形狀變化。一般所說的挫曲就是指此類行為。挫曲分成兩種主要的類型,分別是完美與瑕疵結構的挫曲。
完美結構的挫曲
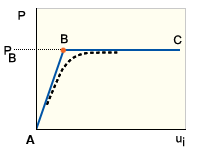
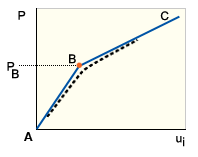
隨著負載的增加,完美結構一開始時會遵循其主要 (或基本) 平衡路徑,即穩定性與挫曲:直柱、穩定性與挫曲:平板和穩定性與挫曲:圓柱薄殼 中的 AB。在此階段中,結構最弱方向 (亦即橫向或平面外方向) 的勁度會穩定下降。在 B 點,即分歧點,結構會跟著阻力最低的 (目前) 線挫曲。可將此形式的挫曲視為從勁度薄膜 (軸向) 支配的路徑轉換為彈性彎曲支配的路徑。由於細長樑與薄壁板及薄殼在軸向上的勁度比彎曲上的勁度高許多,因此它們很自然地最容易發生挫曲。
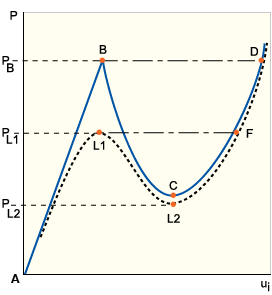
穩定性與挫曲:直柱、穩定性與挫曲:平板和穩定性與挫曲:圓柱薄殼中的路徑 BC 稱為次級或後挫曲路徑。分歧之後的結構穩定性以位於 B 的次級路徑坡度為特徵。因此,B 的平衡狀態為中立 (穩定性與挫曲:直柱)、穩定 (穩定性與挫曲:平板) 及不穩定 (穩定性與挫曲:圓柱薄殼)。
在不穩定的情況下,任何任意小的負載增量都會導致結構立即跳至相鄰穩定平衡規劃 (例如穩定性與挫曲:圓柱薄殼) 中的虛線路徑 BD)。此現象稱為失穩挫曲。請注意另一條後挫曲路徑,如穩定性與挫曲:圓柱薄殼中的 BCD 實線彎曲路徑所示,追蹤了理論上的平衡狀態,如果防止失穩發生,便會出現這種狀態,而負載會逐漸消失,直到在 C 點重新獲得穩定路徑為止。
穩定性與挫曲:直柱
穩定性與挫曲:平板
穩定性與挫曲:圓柱薄殼
很明顯的,從設計師的角度來看,比較希望得到穩定的後挫曲路徑,如果位移保持可以接受的狀態,在可用後挫曲力量中使用增量便不會顯得不尋常了。另一方面,一般很少會接受不穩定的平衡路徑,特別是因為它通常會伴隨著動態失穩。此外,展示不穩定挫曲的結構通常都是對瑕疵敏感的,也就是說,最大或臨界負載容量對很小程度的變化及初始瑕疵形狀都很敏感。
瑕疵結構的挫曲
真實的結構永遠不會完美。即使是幾何圖形、負載、邊界條件或材料性質的些微混亂,都會防止真實的分歧出現。主要與次要路徑並不會相交以形成斜率的中斷,這兩種路徑會局部彎曲以形成一個連續而唯一的解。所產生的後挫曲路徑由穩定性與挫曲:直柱、穩定性與挫曲:平板和穩定性與挫曲:圓柱薄殼中的虛線表示。隨著瑕疵程度的減少,曲率的變化會變得更局部化。完美結構會展示不穩定的分歧點,而瑕疵結構則會展示限制點 ( 穩定性與挫曲:圓柱薄殼中的 L1)。
繼續沿後挫曲路徑向下,我們可能會遇到第二個限制點,但此時它會成為負載撓曲曲線上的最小點 ( 穩定性與挫曲:圓柱薄殼中的 L2)。請注意,與完美結構類似,實際上不會跟在不穩定路徑 L1L2 之後,而是會出現由虛線路徑 L1F 所表示的瞬間失穩挫曲。儘管完美結構的挫曲通常牽涉到分歧,但並非總是如此。當預挫曲模式形狀中包含因強加的邊界條件而無法中斷的對稱時,可能會經由限制點發生不穩定的挫曲。因此,分歧挫曲有時候亦稱為對稱中斷。
分析考量因素
當對包含對稱性的完美結構執行非線性增量分析時,必須為結構指定小型瑕疵,以中斷對稱。如果沒有這樣做,解很可能會繼續沿著基礎平衡路徑走,而不會分支到真實的後挫曲路徑。可能會發生這種情況的例子,如同軸負載下的直柱及平面內負載下的平板。當對沒有冷卻分析結果的平坦部分執行翹曲分析時,有助於您瞭解後者的例子。在此類情況下,建議的程序是建立形狀對應於預期挫曲模式形狀的小型幾何瑕疵。(如果挫曲模式形狀未知,則可使用任何平面外形狀。)