Durchschnittliche Elementdicke
Die 11. Benutzer-Materialkonstante definiert die durchschnittliche Elementdicke für den energiebasierten Zerfall. Bei zweidimensionalen Elementen wird dieser Wert ignoriert. Bei dreidimensionalen (Volumenkörper-)Elementen ist dies die durchschnittliche Dicke der Volumenkörperelemente des Materials, wobei die Dicke definiert ist als die Abmessung des Elements zwischen den Lagen.
Sie erinnern sich aus Anhang A.5, dass sich die letzte effektive Dehnung in energiebasierten Zerfallsberechnungen wie folgt ergibt:
Le ist hierbei die von Abaqus definierte repräsentative Elementlänge. Bei dreidimensionalen Elementen (d. h. Ziegeln und Kontinuumschalen) ist die Länge des Elements die Kubikwurzel des Volumens. Bei zweidimensionalen Elementen (d. h. Schalen und Ebenenspannungselementen) ist die Länge des Elements die Quadratwurzel der Fläche.
Bei zweidimensionalen Elementen wird die Elementdicke ignoriert. Die repräsentative Elementlänge ist ein Maß für die Fläche in der Ebene des Elements, das ein aussagekräftiges Maß für eine Verbundlage liefert. Bei geschichteten Volumenkörperelementen bezieht sich die repräsentative Elementlänge jedoch nicht auf ein Maß für eine einzelne Verbundlage. Um die Nutzung von Volumenkörperelementen und den Vergleich mit den Ergebnissen für zweidimensionale Elemente zu ermöglichen, muss die repräsentative Elementlänge geändert werden, um ein aussagekräftiges Maß für die Länge des Elements in der Ebene einer Verbundlage zu liefern.
Brüche treten in Verbundmaterialien fast immer in der Ebene einer Lage auf. Daher ist es genauer, die Gesamtdicke des Elements zu vernachlässigen. Dies geschieht durch Verwendung der durchschnittlichen Elementdickenkonstanten aus der Materialdefinition. Die repräsentative Elementlänge wird dann wie folgt berechnet:
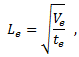
Hierbei ist Ve das Volumen des Elements und te die durchschnittliche Dicke des Elements. Die Elementlänge aus der obigen Gleichung bietet ein genaues Maß der Fläche in der Ebene eines Volumenkörperelements und reduziert sich auf das exakte von Abaqus bereitgestellte Maß für zweidimensionale Elemente, wenn die Dicke eines Volumenkörperelements konstant ist.
Zerfallszeitraum
In Abaqus/Explicit-Analysen mit sofortigem Zerfall kann der sofortige Zerfall der Materialeigenschaften negative Auswirkungen auf das Verhalten der Struktur haben. Lokales Materialverhalten mit hohen Änderungsraten bei der Steifheit kann Schockwellen im Material hervorrufen, die zu vorzeitigem Schadensbeginn in benachbarten Elementen führen können. Um diesen Effekt abzuschwächen, geben wir mithilfe der Benutzer-Materialkonstanten 11 einen Zeitraum für den Zerfall der Materialeigenschaften an. Dieser Wert muss größer oder gleich null sein. Längere Zeiträume führen zu niedrigeren Änderungsraten bei der Steifheit.
Bei Ausfallsbeginn werden die Materialeigenschaften nicht automatisch auf den nächsten Materialzustand reduziert. Die Materialsteifheit wird anhand der folgenden Gleichung aktualisiert:
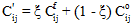
Hierbei sind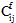 
und 
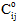die Materialsteifheit im nächsten bzw. vorherigen Materialzustand und 
die aktualisierte (mittlere) Materialsteifheit.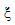 
ist definiert als:
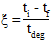
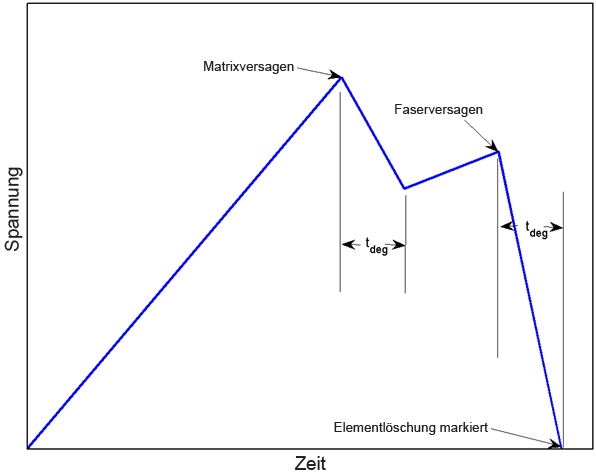
Hierbei sind ti, tf und tdeg jeweils die aktuelle Zeit, die Zeit bei Ausfallsbeginn und der Zerfallszeitraum (Benutzer-Materialkonstante 11). Die Abbildung unten zeigt die lokale Materialreaktion als Zeitfunktion für verschiedene Werte des Zerfallszeitraums (konstante Dehnung nach Ausfallsbeginn).
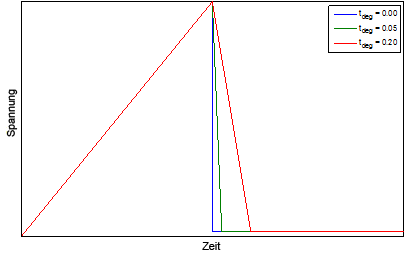
Ein vereinfachtes Beispiel der Spannung an einem Integrationspunkt in Bezug auf Zeit finden Sie im nachfolgenden Diagramm.
