Einige Befehle für die thermischen Ergebnisse sind identisch mit den linearen Ergebnissen.Nachfolgend sind die Befehle aufgeführt, die sich ausschließlich auf thermische Analysen beziehen.
Berechnete Temperatur
(Einheiten: Grad) Dies ist die resultierende Temperatur für den aktuell angezeigten Zeitschritt (transiente Analyse) oder Lastfall (stationäre Analyse).
Ausgangstemperatur
(Einheiten: Grad) Zeigt die Temperatur zum Zeitpunkt 0. Dieser Wert ändert sich nicht bei anderen Zeitschritten oder Lastfällen. Bei stationären Analysen wird diese Temperatur verwendet, um die Materialeigenschaften für temperaturabhängige Materialien zu schätzen.
Die Ausgangstemperatur zeigt die aus einem anderen thermischen Modell gelesenen Temperaturen, die Vorgabeknotentemperatur oder die auf das Modell im FEM-Editor manuell angewendete Ausgangstemperatur. Die Ausgangstemperatur zeigt nicht die angewendeten Lasten wie gesteuerte Temperatur oder Konvektions-Umgebungstemperatur.
Wärmestrom
(Einheiten: Energie/Länge^2/Zeit) Bei Aktivierung basiert die Anzeige auf der Strömungsgröße bzw. der angegebenen globalen Richtung am Elementschwerpunkt. Der Wärmestrom am Schwerpunkt wird anhand des Fourierschen Gesetzes und der Temperaturen an den Knoten berechnet.
Wärmestrom durch Fläche
(Einheiten: Energie/Zeit) Wenn diese Option aktiviert ist, basiert die Anzeige auf dem Wärmestrom senkrecht zur zugeordneten Fläche. Ein positiver Wert gibt an, dass die Wärme durch die Fläche aus dem Element strömt; ein negativer Wert gibt an, dass die Wärme durch die Fläche in das Element strömt.
Der berechnete Wert für den Wärmestrom am Schwerpunkt (hfcg) wird verwendet, um den Wärmestrom der Fläche (H) wie folgt zu berechnen:
H = (Komponente hfcg lotrecht zur Fläche)*(Bereich der Fläche).
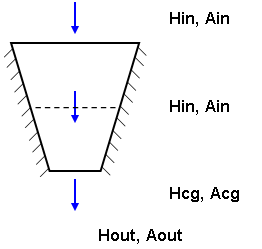
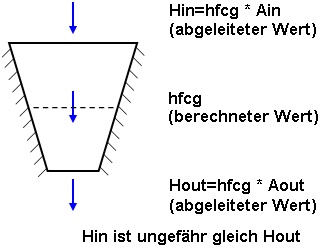
Dies kann dazu führen, dass einige scheinbare Diskrepanzen auftreten, wenn Elemente verzerrt sind oder die Flächen der Elemente nicht parallel und senkrecht zum Wärmestromvektor liegen. Beispiel: Eine Wärme strömt in einem stationären Zustand durch ein trapezförmiges Element mit isolierten Seiten (siehe Abbildung 1(a)). In der Realität entspricht die einströmende Wärme (Hin) der ausströmenden Wärme (Hout). Im FEM-Prozess wird der Wärmestrom am Schwerpunkt berechnet (hfcg), und dann wird der Wärmestrom durch die Flächen abgeleitet. Wie in Abbildung 1(b) gezeigt, führt dies zu einer Näherung, bei der sich für die beiden Wärmeströme leicht unterschiedliche Werte ergeben.
|
|
| (a) In einem hypothetischen Modell ist der Wärmestrom (H) durch jeden beliebigen Bereich gleich, sei es an der Einlassfläche, dem Schwerpunkt (cg) oder dem Auslass. | (b) In FEM wird der Wärmestrom (hfcg), der für den Schwerpunkt berechnet wird, für die Berechnung der Wärmeströme (H) durch die Flächen verwendet. Wenn Ain und Aout nicht gleich Acg sind, dann entspricht die einströmende Wärme nicht der ausströmenden Wärme. |
|
Abbildung 1: - Berechnung des Wärmestroms durch Fläche H = Wärmestrom, A = Bereich, hf = Wärmestrom |
|
Dieses Berechnungsverfahren kann auch zu Situationen führen, in denen der Wärmestrom durch Fläche einen kleinen Wärmewert aufweist, der durch eine adiabatische Wand geht (siehe Abbildung 2), oder wie auf Abbildung 1 zu einer Situation, in der die ausgehende Wärme an der Grenze eines Bauteils nicht gleich der eingehenden Wärme eines anderen Bauteils ist (siehe Abbildung 3). Diese Effekte ergeben sich aufgrund der Näherung bei der Wärmestromberechnung.
Hout = hf n *Bereich der Fläche
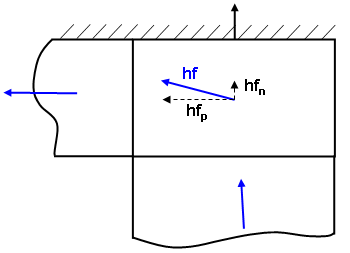
Abbildung 2: Wärmestrom durch Fläche projiziert von Wärmestrom
Bei dem Wärmestrom, der durch eine Fläche geht, wird der Wärmestromvektor (hf) in die Komponenten parallel (hfp) und senkrecht (hfn) zur Fläche aufgegliedert. Es kann scheinen, als verletze die kleine senkrechte Komponente die adiabatische Bedingung. Ein kleineres Netz an der Wand kann zur Minimierung solcher Probleme beitragen. Fügen Sie alternativ eine kleine, unbedeutende Konvektionslast zur adiabatischen Fläche hinzu und legen Sie im Dropdown-Feld Wärmestromberechnung des Dialogfelds Elementdefinition Linear auf Grundlage von BC fest.
 |
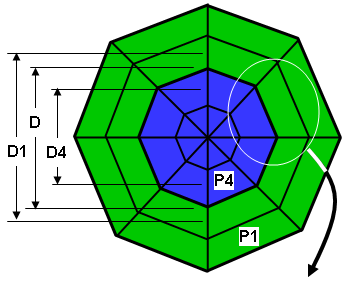(a) Ein Modell aus zwei Bauteilen: Bauteil 1 (grün) auf der Außenseite und Bauteil 4 (blau) auf der Innenseite. Der Durchmesser des Schwerpunkts der inneren Elemente in Bauteil 1 ist D1. Der Durchmesser des Schwerpunkts der äußeren Elemente in Bauteil 4 ist D4. |
 |
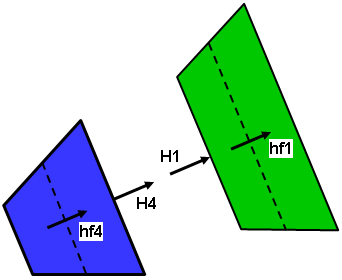(b) Detail von zwei Elementen aus dem Modell, zur Verdeutlichung vergrößert und getrennt. Die Wärmeströme hf4 und hf1 werden anhand der Temperaturverteilung berechnet. Der die Außenfläche von Bauteil 4 (blau) verlassende Wärmestrom ist proportional zu H4 ~ hf4 * D. Der in Bauteil 1 (grün) eingehende Wärmestrom ist proportional zu H1 ~ hf1 * D. Da der Durchmesser D leicht von den Durchmessern der Schwerpunkte D1 und D4 abweicht, an denen der Wärmestrom berechnet wird, sind die beiden Wärmeströme nicht identisch. |
| Abbildung 3: Beispiel für Wärmestrom durch Fläche | |
Für innere Flächen muss die aus einem Element heraus- und in das nächstgelegene Element einströmende Wärme gleich (mit entgegengesetztem Vorzeichen) sein. Der geglättete Wert muss daher Null betragen. Um die Größenordnung des Wärmestroms in dieser Situation anzuzeigen, deaktivieren Sie Ergebniskonturen 
Einstellungen Abgleichungsergebnisse.
Um den Wärmestrom für einen Satz von Flächen zu summieren, wählen Sie Ergebnisse abfragen Abfragen Aktuelle Ergebnisse aus. Wählen Sie die Flächen aus (Auswahl Auswählen Flächen), und ändern Sie dann das Dropdown-Feld Zusammenfassung zu Summe.
- Da zum Ermitteln des Wärmestromergebnisses auch Oberflächen ausgewählt werden können, sollten die Flächen beim Erstellen des Modells auf einer eindeutigen Oberfläche platziert werden. In diesem Fall kann in der Ergebnisanzeige die Oberfläche ausgewählt (Auswahl Auswählen Oberflächen) und die Summe mithilfe des Befehls Ergebnisse abfragen Abfragen Aktuelle Ergebnisse bestimmt werden.
- Wenn auf die summierten Flächen eine Last wie z. B. eine Konvektion oder Strahlung angewendet wird, können Sie die Filtermodule im Browser verwenden, um die Flächenauswahl zu vereinfachen. (Weitere Informationen finden Sie auf der Seite Browser-Funktionen.)
- Der Wärmestrom durch Fläche für eine achsensymmetrische 2D-Analyse ergibt den gesamten Wärmestrom für eine volle Umdrehung (360 Grad = 2*pi).
Für Ziegelelemente werden die äußeren Flächen angezeigt. Um die inneren Flächen anzuzeigen, sollten Sie mit dem Befehl Ergebnisoptionen Ansicht Elemente schrumpfenzwischen den einzelnen Elementen suchen und dann mit dem Befehl Ergebnisoptionen Ansicht Internes Netz anzeigen die inneren Flächen anzeigen.
Wärmestromgenauigkeit
Die Genauigkeit dient zur Hervorhebung von Änderungsstufen in den Ergebnissen zwischen zwei Elementen. In einem idealen Modell ändert sich der Wärmestrom gleichmäßig zwischen angrenzenden Elementen. Bei der Erstellung einer diskreten Auflösung des Modells mit Elementen treten immer gewisse Änderungen in den Ergebnissen von einem Element zum nächsten auf. Die Ergebnisse sind nicht fortlaufend.
In thermischen Analysen basiert die Genauigkeit auf der nicht fortlaufenden Wärmestromgröße von Element zu Element (über Elementgrenzen hinweg). Sie wird wie folgt berechnet:
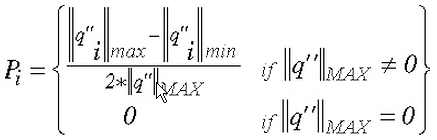
Dabei gilt:
P i ist die Genauigkeit an Knoten i
max
ist die maximale Wärmestromgröße am Knoten i, die durch Ermitteln des Maximums über die benachbarten Elemente erhalten wird
min
ist die minimale Wärmestromgröße am Knoten i, die durch Ermitteln des Minimums über die benachbarten Elemente erhalten wird
MAX
ist das globale Maximum der Wärmestromgröße.
Basierend auf der Formel reicht das Intervall der Genauigkeitswerte von 0 bis 0,5 einschließlich.
Wenn das Modell teilweise ausgeblendet ist, basieren die Genauigkeitsanalysen auf dem eingeschränkten Satz Knoten und Elemente. Knoten, die zu einem einzelnen Element gehören, haben eine Genauigkeit von Null.
Flüssiganteil
Wenn eines der Bauteile einer transienten Wärmeübertragungsanalyse auf ein Phasenwechsel-Materialmodell festgelegt ist, wird die Option Flüssiganteil in Ergebniskonturen Wärmestrom Phasenwechsel angezeigt. Ein Wert von 1 gibt an, dass der Knoten flüssig ist, während der Knoten bei einem Wert von 0 fest ist. Dazwischenliegende Werte geben einen Zustand des Schmelzens bzw. Frierens sowie den flüssigen Anteil der Masse an. Knoten, die zu Bauteilen gehören, für die kein Phasenwechsel-Materialmodell festgelegt ist, werden nicht mit dem Ergebnis schattiert.