La boîte de dialogue Paramètres du solveur itératif s'ouvre lorsque vous cliquez sur le bouton Paramètres dans la boîte de dialogue Préférences de la tâche de l'Analyse de la structure.

Les solveurs itératifs sont utilisés dans les équations lorsque la réorganisation des méthodes de solveurs directs n'est pas efficace et la matrice de rigidité K est suffisamment bien conditionnée. Il s'agit d'outils d'analyse efficaces pour les modèles EF qui comportent des éléments finis pleins et pour les problèmes à grande échelle bien conditionnés. Le temps de calcul augmente considérablement avec les solveurs directs, de même que le problème est plus complexe. L'utilisation de solveurs itératifs permet de réduire la durée de calcul et les exigences en espace disque. Néanmoins, ils présentent quelques inconvénients :
- Leur convergence est lente si des problèmes mal conditionnés sont détectés.
- Chaque cas de charge est calculé de façon itérative depuis le début. Vous devez définir aussi peu de cas de charge que possible.
Pour l'analyse statique linéaire et l'analyse du problème propre (flambement et analyse modale) d'une structure, les solveurs itératifs suivants sont recommandés :
Méthode élément par élément (PCGEBE) et solveur itératif multiniveau (AEBEIS)
Le solveur PCGEBE est utilisé pour tous les types d’éléments finis, son utilisation n’étant pas limitée par la taille du problème. Il est cependant sensible au mauvais conditionnement de la matrice de rigidité K, ce qui peut ralentir la convergence.
Le solveur AEBEIS assure une convergence rapide pour la plupart des problèmes. Il garantit une convergence stable pour les problèmes mal conditionnés. Il est possible d'appliquer des éléments 2D et 3D, tous les éléments plaque et coque surfaciques et tous les types d'éléments pleins. D'autres composantes de la structure telles que les appuis élastiques, les excentrements, les relâchements et les assemblages rigides, peuvent aussi être appliquées. Ce solveur a été implémenté en combinant le solveur d'agrégation sur la base de la technique EBE.
Type de solveur
Sélectionnez un type de solveur :
- Multiniveau désactivé : PCGEBE
- Multiniveau activé - AEBEIS (recommandé)
Sélectionnez ensuite un type de préconditionneur.
Types de préconditionneurs
Les méthodes PCGEBE et AEBEIS reposent sur la technique EBE avec les types de méthodes de préconditionnement suivantes :
- Diagonale : méthode de Jacobi
- Cholesky : préconditionnement symétrique EBE Cholesky
- Gauss : préconditionnement symétrique EBE Cholesky-Gauss-Seidel
- ICCF : technique de factorisation Cholesky incomplète (recommandée)
Tolérance
Définissez les itérations successives (tolérance) exécutées jusqu'à la satisfaction de la condition suivante :
|| rk || / || b || ≤ tol
rk= b - K xk
La norme d’Euclide et la norme uniforme sont prises comme norme vectorielle. Par exemple :
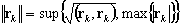
rk= vecteur résiduel
b= côté droit (vecteur de charge)
Xk= approximation de la solution dans la k-ième étape de l’itération. Le paramètre en question définit la précision de l’itération. Si l’on prend tol=0.001, cela signifie que les trois premiers chiffres au moins de la valeur de la réaction seront identiques à celles calculées par le solveur exact (méthode frontale ou skyline). Il est recommandé de supposer tol=0.001 pour une solution de test et tol = {1.0e-04 - 1.0e-08} pour une solution définitive.
Calcul de la matrice K
Si l'option Calcul de la matrice K est activée, les matrices correspondantes pour les éléments finis Ke (e € 1, Nele ; où Nele est le nombre d'éléments finis dans la structure étudiée) sont calculées chaque fois que le produit de la matrice et du vecteur Kv est calculé.
Si l’option Calcul de la matrice K est désactivée, les matrices des éléments finis Ke respectifs (e € 1, Nele) sont prises à partir du disque.
L’option Calcul de la matrice K est ignorée dans ICCF, mais elle fonctionne pour les préconditionneurs suivants :
- Diagonale
- EBE Gauss
- EBE Cholesky
Paramètres de solveur multiniveau
Définissez le nombre de niveaux d'agrégation. La valeur par défaut 1 garantit le nombre d'itérations minimal. Ces calculs complexes nécessitent davantage d'espace disque et un temps de traitement plus long.
Il est conseillé de prendre :
| Nombre d'équations | Nombre d'agrégations |
|---|---|
| < 20 000 | 1 |
| 20 000 - 50 000 | 2 |
| 50 - 200 000 | 3-4 |
| > 200 000 | 4-5 |
Les problèmes de petite taille au niveau le plus approximatif (SPCL, small size of problem on coarsest level) assurent des itérations rapides. Toutefois, un petit SPCL augmente le nombre d'itérations.
Définissez le nombre d'itérations internes effectuées durant le processus de lissage. Sa valeur est généralement égale à 3 ou 4. Lors de l'analyse des tâches volumineuses, vous pouvez augmenter le nombre d'itérations internes jusqu'à 8.
L'activation de l'analyse de la diagonale améliore l'agrégation par le biais de la matrice de rigidité K. Il est conseillé d'activer cette option pour accélérer la convergence.
Méthodes
Les préconditionneurs Diagonale, EBE Gauss et EBE Cholesky peuvent utiliser n'importe laquelle de ces méthodes, tandis qu'ICCF utilise la Méthode 0.
Méthode 0 : solveur à deux niveaux associé aux itérations les plus rapides. La convergence est la plus lente par rapport au nombre d’itérations.
Méthode 1 : solveur multiniveau avec des possibilités de lissage limitées. Pour cette approche, l’utilisation de la mémoire est moins importante pour résoudre les problèmes importants. C'est une excellente alternative à la Méthode 2 lorsque les possibilités matérielles sont limitées.
Méthode 2 : solveur multiniveau utilisant le lissage à chaque niveau d’agrégation. Sa convergence est la meilleure et elle permet d’obtenir le plus grand nombre de niveaux d’agrégation. Les exigences relatives à l’espace disque sont le moins importantes dans ce cas. Il est conseillé d’utiliser cette méthode si le nombre de niveaux d’agrégation est supérieur à 2.
Gestion de la mémoire
Ajustez la mémoire tampon utilisée pour stocker les matrices d'éléments et les éléments de préconditionnement dans la section de gestion de la mémoire. Cette option fonctionne pour les types de préconditionnement suivants : Diagonale, EBE Gauss et EBE Cholesky. La gestion de la mémoire selon l'approche ICCF est ignorée.
min : garantit la taille minimale de la zone tampon, mais peut également réduire la vitesse de calcul (paramètre par défaut).
1/4 : un quart de la mémoire système alloué aux calculs.
1/2 : la moitié de la mémoire système allouée aux calculs.
max : autant de mémoire système que nécessaire allouée aux calculs.
Dépannage
Pour améliorer le temps nécessaire à l'exécution des calculs :
- réduisez le nombre de niveaux d’agrégation
- augmentez le nombre d’itérations internes
- activez l'option Analyse de la diagonale
- utilisez la Méthode 1 ou de préférence la Méthode 2 si plusieurs niveaux d'agrégation sont implémentés
Il est possible de bloquer le préconditionnement pour une méthode multiniveau, ce qui ralentit la convergence. Si le nombre d’itérations dépasse la valeur limite bv=40*lg(tol) et que la tolérance exigée n’a pas été obtenue, cela signifie une convergence lente pour les méthodes multiniveaux. (Ce critère est incorrect pour les méthodes non multiniveaux). Pour y remédier :
- augmentez le nombre d’itérations internes à 8
- réduisez le nombre de niveaux d'agrégation, mais sans dépasser la valeur maximale du niveau le moins précis
- sélectionnez la méthode ICCF ou toute autre méthode non-multiniveau
Meilleures pratiques
Vous pouvez vérifier l'exactitude de chaque élément de la matrice Ke dans le modèle. Cette vérification n’exige pas beaucoup de temps et est recommandée avant de procéder à l’analyse préliminaire du modèle par éléments finis.
- Ouvrez la boîte de dialogue Préférences de la tâche.
- Sélectionnez l'onglet Analyse de la structure.
- Sélectionnez l'option Itérative.
- Cliquez sur Préférences.
- Désélectionnez l'option Multiniveau.
- Sélectionnez l’option EBE Gauss ou EBE Cholesky.
- Cliquez deux fois sur OK.
- Lancez l’analyse de la structure.
Si la procédure de calcul atteint la première itération, cela signifie qu'elle se déroule correctement et qu’on peut arrêter les calculs.
Si la vérification est incorrecte, l’erreur 3016 se produira lors du préconditionnement EBE et les calculs seront arrêtés avant le début des itérations.
Rubrique connexe :
Paramètres du solveur itératif - informations générales
Solveurs disponibles dans le logiciel Robot
Conseils pratiques relatifs à la sélection des paramètres des solveurs itératifs