L'application du solveur itératif est recommandée pour la résolution de tâches statistiques linéaire (15 000 - 1 000 000 équations) et de problèmes à valeurs propres (analyse modale ou de flambement). Les méthodes directes traditionnelles (frontale, skyline, sparse) sont très gourmandes en temps et requièrent une grande quantité d'espace disque disponible pour stocker une matrice factorisée. Cette approche peut être très efficace pour l'analyse de structures contenant un solide FE. Des solveurs de ce type peuvent s'avérer très utiles en analyse statique linéaire (recherche de paramètres de dimensionnement optimaux, par exemple), lorsqu'il est possible d'obtenir les solutions d'approximation pour un petit nombre de cas de charge. Le contrôle élément par élément de l'exactitude des données de régularisation Vinget (comme illustré ci-dessous) constitue une application supplémentaire du solveur itératif qui vous permet de détecter des difficultés d'identification des erreurs dans le MEF.
La méthode PCG (gradient préconditionné), qui intègre plusieurs types de préconditionnements, est en cours de mise en oeuvre.
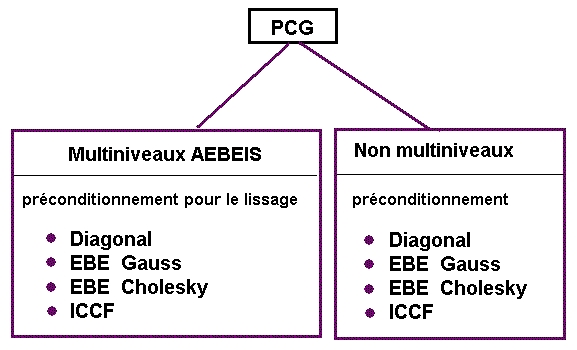
- AEBEIS : Agrégation - Solveur itératif élément par élément 1,2
- EBE : Élément par élément
- ICCF : Approche incomplète - factorisation Cholesky
AEBEIS est un solveur multiniveau, d'agrégation, élément par élément qui combine les avantages des méthodes d'itération rapide à la technique EBE économique. Il autorise l'accélération d'opérations de base via une approche économique par rapport aux exigences en termes de mémoire requise. Les approches de type agrégation comme celle-ci autorisent une analyse de solides, de coques (à l'instar des méthodes "multi-grid"), de barres et de structures composées de barres, de coques et de solides.
D'une manière générale, AEBEIS permet d'accélérer la convergence par rapport aux méthodes à un seul niveau. Il n'est limité qu'aux structures 3D et aux portiques 2D. AEBEIS est moins sécurisée mais est peu sensible aux problèmes mal conditionnés relatifs à des méthodes itératives pertinentes, non-multiniveau. Dans de rares cas, un "verrouillage" de préconditionnement est mis en place, tandis que la convergence est toujours lente.
AEBEIS permet l'application d'éléments de barre 2D et 3D, d'élément de coque (3, 4, 6 et 8 éléments de nœud ), d'éléments solide. Il permet également d'éléments de composants de structure supplémentaire comme des appuis élastiques, des décalages, des relâchements et les liaisons rigides. Il n'existe aucune restriction concernant les types d'élément ou de structure pour une méthode non-multiniveau.
Les types suivants de préconditionnement sont disponibles dans les deux approches AEBEIS et non-multiniveau.
- Diagonale - Préconditionnement Jacobi (ne s'applique qu'à des problèmes bien conditionnés).
- EBE Gauss - Préconditionnement EBE Gauss-Seidel-Cholesky modifié 1,2 .
- EBE Cholesky - Préconditionnement EBE Cholesky 1,4 .
- ICCF - Approche incomplète - factorisation Cholesky 5,6 .
L'approche ICCF est plus rapide que d'autres méthodes (diagonale, EBE Gauss, EBE Cholesky) et utilise approximativement le même nombre d'itérations pour obtenir la convergence, tels que les approches EBE Gauss ou EBE Cholesky. Elle n'utilise pas les opérations d'E/S du disque, mais requiert davantage de mémoire RAM. ICCF est recommandée si l'ordinateur dispose d'une quantité de mémoire RAM suffisante pour la tâche. Les exigences en termes de mémoire RAM et d'espace disque requis pour les approches EBE Gauss et EBE Cholesky sont minimes, mais ces dernières sont plus lentes que l'approche ICCF.
Références
- Fialko S.Yu. High-performance aggregation element-by-element iterative solver for large-scale complex shell structure problems. Archives of Civil Engineering, XLV, 2, 1999. P.193-207.
- Fialko S., High-performance aggregation element-by-element Ritz-gradient method for structure dynamic response analysis, CAMES, 7: 537-550, 2000.
- Hughes T.J.R., Ferencz M. Implicit solution of large-scale contact and impact problems employing an EBE preconditioned iterative solver, IMPACT 87 Int. Conference on Effects of Fast Transient Loading in the Context of Structural Mechanics, Lausanne, Suisse, août 26-27, 1987.
- Hughes T.J.R., R.M.Ferencz et j.O.Hallquist. Large-scale vectorized implicit calculations in solid mechanics on a CRAY X-MP/48 utilizing EBE preconditioned conjugate gradients, Comput. Meths. Appl. Mech. Engrg., 61.
- S.Bitzarakis, M.Papadrakakis, A.Kotsopulos. Parallel solution techniques in computational structural mechanics. Comp. Methods Appl. Mech. Engrg. 1997, 148, p.75-104.
- M.Papadrakakis, Solving large - scale problems in mechanics, John Wiley & Sons Ltd., 1993.
Rubrique connexe :
Paramètres du solveur itératif
Solveurs accessibles dans Robot
Conseils pratiques relatifs à la sélection des paramètres des solveurs itératifs