Parametry solwera iteracyjnego

Po naciśnięciu przycisku Parametry znajdującego się w oknie dialogowym Preferencje zadania na ekranie pojawia się okno Parametry solwera iteracyjnego.

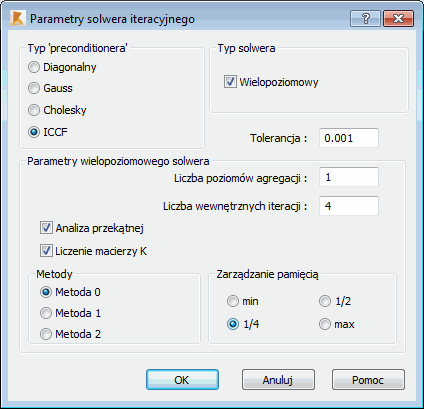
Solwery iteracyjne stosuje się w równaniach, gdy metody renumeracji dla solwerów bezpośrednich nie są zbyt wydajne, a macierz sztywności K jest wystarczająco dobrze uwarunkowana. Solwery iteracyjne są bardzo wydajne dla modeli zawierających elementy skończone (w tym elementy objętościowe) i dla dobrze uwarunkowanych dużych problemów. Czas obliczeń dla solwerów bezpośrednich gwałtownie wzrasta, gdy zwiększony zostanie rozmiar problemu. Zazwyczaj użycie solwerów iteracyjnych pozwala na znaczne zmniejszenie czasu obliczeń oraz wymogów dotyczących zasobów dysku. Należy jednak zwrócić uwagę na pewne wady solwerów iteracyjnych.

W przypadku liniowej analizy statycznej i analizy drgań własnych konstrukcji (wyboczenia i analiza modalna) zaleca się następujące solwery iteracyjne.

Elemen-na-element (PCGEBE) i wielopoziomowy solwer iteracyjny (AEBEIS)

Solwer PCGEBE jest używany dla wszystkich typów elementów skończonych i nie posiada ograniczeń związanych z rozmiarem rozwiązywanego problemu. Jest natomiast wrażliwy na złe uwarunkowanie macierzy sztywności K - możliwa jest powolna zbieżność.

Solwer AEBEIS cechuje szybka zbieżność dla większości problemów. Charakteryzuje się również bardziej stabilną zbieżnością dla problemów źle uwarunkowanych. Istnieje możliwość stosowania dla płaskich (2D) i przestrzennych (3D) elementów prętowych, wszystkich typów powierzchniowych elementów płytowo/powłokowych i wszystkich typów elementów bryłowych. Dodatkowo, można również zastosować elementy komponentów konstrukcji, takie jak: elastyczne podpory, odsunięcia, zwolnienia i sztywne połączenia. Ten solwer realizuje połączenie solwera agregacyjnego na podstawie techniki EBE.

Typ solwera

Należy wybrać typ solwera:

Następnie należy wybrać typ preconditionera.

Typy preconditionera:

Metody PCGEBE oraz AEBEIS opierają się na technice EBE z zastosowaniem następujących metod uwarunkowania wstępnego:

Tolerancja

Definicja kolejnych iteracji (tolerancja) jest konieczna aż do spełnienia następującego warunku:

|| rk || / || b || ≤ tol

rk= b - K xk

Jako wektor normalny przyjęto maksimum Euklidesa i normalną. Na przykład:

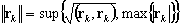
rk= wektor resztkowy

b= po prawej stronie (wektor obciążenia)

Xk - aproksymacja rozwiązania na k-tym kroku iteracji. Ten parametr określa precyzję iteracji. Jeśli przyjmiemy, że tol=0.001, to oznacza to, że co najmniej trzy pierwsze cyfry wartości reakcji będą takie same jak w rozwiązaniu ścisłym otrzymanym przy wykorzystaniu dokładnego solwera (metoda frontalna lub skyline). Zaleca się przyjmowanie tol=0.001 dla rozwiązania próbnego i tol = {1.0e-04 - 1.0e-08} dla rozwiązania ostatecznego.

Liczenie macierzy K

Jeżeli opcja Liczenie macierzy K jest włączona, to odpowiadające macierze dla elementów skończonych Ke (e € 1, Nele, gdzie Nele jest liczbą elementów skończonych w rozważanej konstrukcji) są obliczane za każdym razem, gdy obliczany jest iloczyn macierzy i wektora Kv;

jeśli opcja Liczenie macierzy K jest wyłączona, to macierze elementów skończonych Ke (e Î 1, Nele) są brane z dysku.

Uwaga: Włączenie opcji jest zalecane, gdy użytkownik posiada bardzo szybki procesor i stosunkowo wolny dostęp do dysku. W innym przypadku zaleca się wyłączenie tej opcji.

Jest pomijana w przypadku podejścia ICCF, ale można z niej korzystać w przypadku następujących preconditionerów:

Uwaga: Wymienione powyżej parametry muszą być określone zarówno dla solwera PCGEBE, jak i solwera AEBEIS. Opisane poniżej parametry należy zdefiniować jedynie w przypadku, gdy wybrany został solwer AEBEIS.

Parametry solwera wielopoziomowego

Należy zdefiniować liczbę poziomów agregacji. Domyślna wartość parametru zapewnia minimalną liczbę iteracji. Te złożone obliczenia wymagają więcej miejsca na dysku i czasu.

Zaleca się przyjęcie:

Liczba równań Liczba poziomów agregacji
< 20 000 1
20 000 — 50 000 2
50 — 200 000 3 — 4
> 200 000 4 — 5

Należy pamiętać, że odpowiednio mały rozmiar problemu na zgrubnym poziomie (SPCL, small sized problems at the coarsest level) zapewnia szybkie iteracje. Z drugiej strony, im mniejszy SPCL, tym większa liczba iteracji.

Liczba wewnętrznych iteracji — opcja ta określa liczbę wewnętrznych iteracji podczas wygładzania. Wartość tego parametru zazwyczaj wynosi 3 lub 4. W pewnych przypadkach, mających zwykle miejsce podczas analizy dużych zadań, może zajść konieczność zwiększenia liczby wewnętrznych iteracji do 8.

Analiza przekątnej — włączenie tej opcji powoduje poprawienie agregacji poprzez analizę przekątnej macierzy sztywności K. Zaleca się włączenie tej opcji, aby przyspieszyć zbieżność.

Metody

Preconditionery ukośny, EBE Gaussa i EBE Cholesky'ego mogą wykorzystywać każdą z podanych metod. Przy podejściu ICCF zawsze używana jest Metoda 0.

Metoda 0 jest solwerem dwupoziomowym. Charakteryzuje się najszybszymi iteracjami w porównaniu z innymi metodami, ale odznacza się najwolniejszą zbieżnością w odniesieniu do liczby iteracji.

Metoda 1 jest wielopoziomowym solwerem z ograniczonymi możliwościami wygładzania. To podejście zapewnia mniejsze wykorzystanie pamięci w porównaniu z Metodą 2; może być używane do rozwiązywania dużych problemów, jeżeli ze względu na możliwości komputera nie jest możliwe użycie Metody 2.

Metoda 2 jest wielopoziomowym solwerem z wykorzystaniem wygładzania na każdym poziomie agregacji. Zazwyczaj charakteryzuje się najlepszą zbieżnością i pozwala na utrzymanie maksymalnej liczby poziomów agregacji. Prowadzi to do minimalnych wymagań związanych z pamięcią dyskową. Zaleca się używanie tej metody w przypadku, gdy liczba poziomów agregacji jest większa niż 2.

Uwaga: Jeżeli liczba poziomów agregacji równa się 1, to wszystkie metody działają w taki sam sposób.

Zarządzanie pamięcią

Opcja Zarządzanie pamięcią określa wielkość bufora służącego do przechowywania macierzy elementów i elementów preconditionera. Ta opcja działa dla następujących typów uwarunkowania wstępnego: Diagonal, EBE Gauss i EBE Cholesky. W podejściu ICCF jest pomijana.

min: zapewnia minimalną wielkość bufora, ale może zmniejszyć szybkość obliczeń (ustawienie domyślne).

1/4: jedna czwarta pamięci systemowej przeznaczonej dla obliczeń.

1/2: połowa pamięci systemowej przeznaczonej dla obliczeń.

max: cała pamięć systemowa przeznaczona dla obliczeń.

Uwaga: Wykorzystywanie połowy lub całej pamięci fizycznej może prowadzić do problemów z obsługą innych programów.

Rozwiązywanie problemów

W celu skrócenia czasu potrzebnego do obliczeń zalecane jest:

Dla pewnych przypadków możliwe jest „zablokowanie" uwarunkowania wstępnego dla metody wielopoziomowej. Prowadzi to do powolnej zbieżności. Jeżeli liczba iteracji przekracza wartość graniczną bv=40*lg(tol) i żądana tolerancja nie została osiągnięta, to oznacza to powolną zbieżność dla metody wielopoziomowej. (Takie kryterium nie jest poprawne w przypadku metod niewielopoziomowych). W takich przypadkach zaleca się przeprowadzenie następujących operacji:

Wzorce postępowania

Poprawność każdego elementu matrycy Ke w modelu może zostać sprawdzona. Taka weryfikacja nie jest czasochłonna i zalecane jest jej przeprowadzenie przed analizą próbną modelu elementów skończonych. Aby tego dokonać, należy:

  1. Otworzyć okno Preferencje zadania.
  2. Przejść na kartę Analiza konstrukcji.
  3. Wybrać opcję Iteracyjne.
  4. Kliknąć przycisk Preferencje.
  5. Wyłączyć opcję Wielopoziomowa.
  6. Wybrać jedną z opcji: EBE Gauss lub EBE Cholesky.
  7. Kliknij dwa kolejne przyciski OK.
  8. Uruchomić analizę konstrukcji.

Jeżeli proces obliczeniowy dojdzie do pierwszej iteracji, to oznacza to, że przebiega on prawidłowo i można przerwać obliczenia.

Jeżeli weryfikacja nie jest poprawna, to podczas przygotowywania ‘preconditioning’ EBE wystąpi błąd 3016 i obliczenia zostaną przerwane, zanim rozpocznie się proces iteracji.

Patrz również:

Parametry solwera iteracyjnego — informacje ogólne

Solwery dostępne w programie Robot

Zalecenie praktyczne dotyczące wyboru parametrów solwerów iteracyjnych

Temat nadrzędny: Analiza konstrukcji